Question

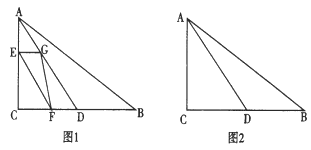
【题目】如图1，△ABC中，∠ACB=90°，AC=4cm，BC=6cm，D是BC的中点.点E从A出发，以acm/s(a＞0)的速度沿AC匀速向点C运动；点F同时以1cm/s的速度从点C出发，沿CB匀速向点B运动，其中一个动点到达端点时，另一个动点也随之停止运动，过点E作AC的垂线，交AD于点G，连接EF，FG，设它们运动的时间为t秒(t≥t0).

(1)若t=2，△CEF∽△ABC，求a的值；

(2)当a=时，以点E、F、D、G为顶点点四边形时平行四边形，求t的值；

(3)若a=2，是否存在实数t，使得点△DFG是直角三角形？若存在，请求出t的值；若不存在，请说明理由．

Answer 1

【答案】(1)；(2)或；(3)t=，△DFG是直角三角形．

【解析】

（1）根据相似三角形的性质，建立比例关系，进而求解.（2）根据相似三角形的定义证明△AEG∽△ACD，进而得到 ，求得EG的值，再根据题意求出t的取值.（3）根据题意及勾股定理，再结合（2）中△AEG∽△ACD，得到 ，最后分情况讨论，得出t=，△DFG是直角三角形.

(1)∵t=2，

∴CF=2厘米，AE=2a厘米，

∴EC=(4﹣2a ) 厘米，

∵△ECF∽△BCA．

∴．

∴

∴．

(2)由题意，AE=t厘米，CD=3厘米，CF=t厘米．

∵EG∥CD

∴△AEG∽△ACD．

∴，

∴EG=．

∵以点E、F、D、G为顶点的四边形是平行四边形

∴EG=DF．

当0≤t＜3时，

∴．

当3＜t≤6时，

∴．

综上，或.

(3)∵点D是BC中点

∴CD=BC=3，

在Rt△ACD中，根据勾股定理得，AD=5，

由题意，AE=2t厘米，CF=t厘米，

由(2)知，△AEG∽△ACD，

∴，

∴

∴AG=厘米，EG=，DF=3﹣t厘米，DG=5﹣(厘米)．

若∠GFD=90°，则EG=CF，=t．

∴t=0，(舍去)(11分)若∠FGD=90°，则△ACD∽△FGD．

∴，

∴．

∴t=．

综上：t=，△DFG是直角三角形．