题目内容
【题目】在平面直角坐标系中,O为坐标原点,点A(a,a)在第一象限,点B(0,b),点C(3,0),
其中0<b<3,∠BAC=90°.
(1)根据题意,画出示意图;
(2)若a=2,求OB的长;
(3)已知点D在线段OB的上,若![]() ,四边形OCAD的面积为3,求
,四边形OCAD的面积为3,求![]() 的值.
的值.
【答案】(1)见详解(2)1(3)2
【解析】
(1)根据题意画出图形即可;
(2)由勾股定理表示出BC2=c2+9,AC2=(2-c)2+4,AB2=1+4=5,根据AB2+AC2=BC2,即5+(2-c)2+4=c2+9,解之可得c的值;
(3)过点A作AE⊥x轴于点E,作AF⊥y轴于点F,OF=OE=AF=AE=a,∠AEC=∠AFB=90°,由△ACE≌△ABF知BF=CE=3-a、OC=2a-3,根据OB2-OC2=8S△CAD得CD=3-a、OD=OC-CD=3a-6,最后由S四边形OBAD=S△OAB+S△OAD可得关于a的方程,变形可得答案.
解:(1)
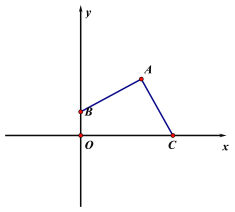
(2)
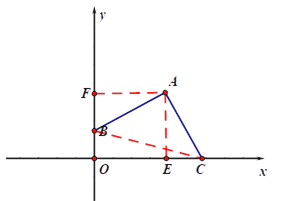
如图,
过点A作AF⊥y轴于点F,AE⊥x轴于点E.
若a=2,则A(2,2),
连接BC,则在Rt△BOE中,BC2= OB2+OC2=b2+9,
在Rt△AEC中AC2= AE2+EC2=22+(3-2)2=5,
在Rt△AFB中AB2= AF2+BF2=22+(2-b)2,
∵∠BAC=90°,
∴在Rt△ABC中,AB2+AC2=BC2,
即22+(2-b)2+5= b2+9,
解得:b=1,
即OB= b=1;
(3)
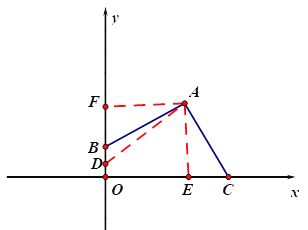
过点A作AE⊥x轴于点E,作AF⊥y轴于点F,连接AD.
由平面直角坐标系知:OF=OE=AF=AE=a,∠AEC=∠AFB=90°,
∵∠BAC=∠CAE+∠BAE=90°,∠FAE=∠FAB+∠BAE=90°,
∴∠CAE=∠FAB,
在△ACE和△ABF中,
∴△ACE≌△ABF(AAS),
∴BF=CE=3-a,
∴OB=OF-BF=a-(3-a)=2a-3
∵OC=3,![]() ,
,
∴9-(2a-3)2=8![]()
即![]() =
=![]()
∵S四边形OCAB =S四边形OCAD+![]()
S四边形OCAB= S四边形OEAB+S △ACE
△ACE≌△ABF,
∴S四边形OCAD+![]() = S四边形OEAB+S △ACE= S四边形OEAB+S △ABF= S四边形OEAF=a2
= S四边形OEAB+S △ACE= S四边形OEAB+S △ABF= S四边形OEAF=a2
∵四边形OCAD的面积为3
∴3+![]() = a2
= a2
化简得:![]()