题目内容
【题目】【阅读材料,获取新知】
善于思考的小军在解方程组![]() 时,采用了一种“整体代换法”的解法.
时,采用了一种“整体代换法”的解法.
解:将方程(2)变形:4x+10y+y=5即2(2x+5y)+y=5(3)
把方程(1)代入(3)得:2×3+y=5
∴y=﹣1.
把y=﹣1,代入(1)得x=4
∴方程组的解为 ![]()
【利用新知,解答问题】
请你利用小军的“整体代换法”解决一下问题:
(1)解方程组:
① ![]() ②
② 
(2)已知x,y满足方程组 ![]() ,则x2+4y2与xy的值分别为、 .
,则x2+4y2与xy的值分别为、 .
【答案】
(1)解:① ![]()
由②得:3(3x﹣2y)+2y=19③,
把①代入③得:15+2y=19,
解得:y=2,把y=2代入①得:3x﹣4=5,
解得:x=3,
所以原方程组的解为 ![]() ;
;
② 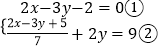
由①得:2x﹣3y=2③,
把③代入②得:1+2y=9,
解得:y=4,
把y=4代入①得:2x﹣12﹣2=0,
解得:x=7,
所以原方程组的解为 ![]()
(2)17,2
【解析】(2) ![]() ,
,
原方程组化为: ![]() ,
,
①+2×②得:7(x2+4y2)=119,
即x2+4y2,=17,
把x2+4y2,=17代入①得:51﹣2xy=47,
解得:xy=2,
所以答案是:17,2;
整体代换就是变形其中一个方程使其出现另一个方程的未知数部分,将其值代入求得.
【考点精析】解答此题的关键在于理解代数式求值的相关知识,掌握求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入.

【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
根据以上信息解决下列问题:
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | 20 |
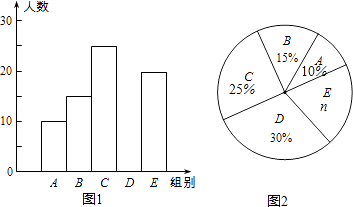
(1)在统计表中,m= , n= , 并补全直方图;
(2)扇形统计图中“C组”所对应的圆心角的度数是度;
(3)若该校共有964名学生,如果听写正确的个数少于24个定为不合格,请你估算这所学校本次比赛听写不合格的学生人数.