题目内容
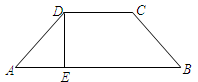
如图,在四边形ABCD中,DB平分∠ADC,∠ABC=120°,∠C=60°,∠BDC= ;延长CD到点E,连接AE,使得∠E=
;延长CD到点E,连接AE,使得∠E= ∠C.
∠C.

(1)求证:四边形ABDE是平行四边形;
(2)若DC=12,求AD的长.
 ;延长CD到点E,连接AE,使得∠E=
;延长CD到点E,连接AE,使得∠E= ∠C.
∠C.
(1)求证:四边形ABDE是平行四边形;
(2)若DC=12,求AD的长.
(1)见解析 (2)6
(1)证明:∵∠ABC=120°,∠C=60°,
∴ ∠ABC+∠C=180°,
∴ AB∥DC,即AB∥ED.
又∵∠C=60°,∠E=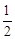 ∠C,∠BDC=30°,
∠C,∠BDC=30°,
∴∠E=∠BDC=30°,∴ AE∥BD.
∴ 四边形ABDE是平行四边形.
(2)解:由(1)得AB∥DC,AB≠DC,
∴ 四边形ABCD是梯形.
∵ DB平分∠ADC,∠BDC=30°,
∴∠ADC=∠C=60°.
∴ 四边形ABCD是等腰梯形,
∴BC=AD.
∵在△BCD中,∠C=60°,∠BDC=30°,
∴∠DBC=90°.
又已知DC=12,∴ AD=BC=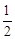 DC=6.
DC=6.
∴ ∠ABC+∠C=180°,
∴ AB∥DC,即AB∥ED.
又∵∠C=60°,∠E=
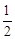 ∠C,∠BDC=30°,
∠C,∠BDC=30°,∴∠E=∠BDC=30°,∴ AE∥BD.
∴ 四边形ABDE是平行四边形.
(2)解:由(1)得AB∥DC,AB≠DC,
∴ 四边形ABCD是梯形.
∵ DB平分∠ADC,∠BDC=30°,
∴∠ADC=∠C=60°.
∴ 四边形ABCD是等腰梯形,
∴BC=AD.
∵在△BCD中,∠C=60°,∠BDC=30°,
∴∠DBC=90°.
又已知DC=12,∴ AD=BC=
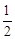 DC=6.
DC=6.
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 中,
中, ∥
∥ ,
, 分别是
分别是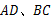 的中点,
的中点, 分别是
分别是 的中点.
的中点.
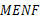 是菱形;
是菱形; 的高和底边
的高和底边


 ,∠
,∠ ,DE⊥AB于点E,且
,DE⊥AB于点E,且 ,那么梯形ABCD的周长为_______,面积为________.
,那么梯形ABCD的周长为_______,面积为________.