ЬтФПФкШн
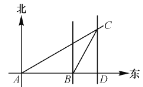
ЁОЬтФПЁПХзЮяЯпy=-x2+2x+3гыxжсЯрНЛгкAЃЎBСНЕуЃЈЕуAдкBЕФзѓВрЃЉЃЌгыyжсЯрНЛгкЕуCЃЌЖЅЕуЮЊD.
ЃЈ1ЃЉжБНгаДГіA,B,CШ§ЕуЕФзјБъКЭХзЮяЯпЕФЖдГЦжсЃЛ
ЃЈ2ЃЉСЌНгBCЃЌгыХзЮяЯпЕФЖдГЦжсНЛгкЕуEЃЌЕуPЮЊЯпЖЮBCЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїPF//DEНЛХзЮяЯпгкЕуFЃЌЩшЕуPЕФКсзјБъЮЊmЃК
ЂйгУКЌmЕФДњЪ§ЪНБэЪОЯпЖЮPFЕФГЄЃЌВЂЧѓГіЕБmЮЊКЮжЕЪБЃЌЫФБпаЮPEDFЮЊЦНааЫФБпаЮЃП
ЂкЩшЁїBCFЕФУцЛ§ЮЊSЃЌЧѓSгыmЕФКЏЪ§ЙиЯЕЪНЃЎ
ЁОД№АИЁПЃЈ1ЃЉAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉЃЛХзЮяЯпЕФЖдГЦжсЪЧЃКx=1ЃЎЃЈ2ЃЉЂйЕБm=2ЪБЃЌЫФБпаЮPEDFЮЊЦНааЫФБпаЮЃЛЂк![]() .
.
ЁОНтЮіЁПЪдЬтЗжЮі: ЃЈ1ЃЉЖдгкХзЮяЯпНтЮіЪНЃЌСюy=0ЧѓГі![]() ЕФжЕЃЌШЗЖЈГіAгыBзјБъЃЌСюx=0ЧѓГі
ЕФжЕЃЌШЗЖЈГіAгыBзјБъЃЌСюx=0ЧѓГі![]() ЕФжЕШЗЖЈГі
ЕФжЕШЗЖЈГі![]() зјБъЃЌНјЖјЧѓГіЖдГЦжсМДПЩЃЛ
зјБъЃЌНјЖјЧѓГіЖдГЦжсМДПЩЃЛ
ЃЈ2ЃЉЂйИљОн![]() гы
гы![]() зјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈШЗЖЈГіжБЯп
зјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈШЗЖЈГіжБЯп![]() НтЮіЪНЃЌНјЖјБэЪОГі
НтЮіЪНЃЌНјЖјБэЪОГі![]() гы
гы![]() зјБъЃЌИљОнХзЮяЯпНтЮіЪНШЗЖЈГі
зјБъЃЌИљОнХзЮяЯпНтЮіЪНШЗЖЈГі![]() гы
гы![]() зјБъЃЌБэЪОГі
зјБъЃЌБэЪОГі![]() ЃЌРћгУЦНааЫФБпаЮЕФХаЖЈЗНЗЈШЗЖЈГі
ЃЌРћгУЦНааЫФБпаЮЕФХаЖЈЗНЗЈШЗЖЈГі![]() ЕФжЕМДПЩЃЛ
ЕФжЕМДПЩЃЛ
ЂкСЌНг![]() ЃЌЩшжБЯп
ЃЌЩшжБЯп![]() гыxжсНЛгкЕуM,ЃЌЧѓГі
гыxжсНЛгкЕуM,ЃЌЧѓГі![]() ЕФГЄЃЌИљОн
ЕФГЄЃЌИљОн![]() ,СаГі
,СаГі![]() Йигк
Йигк![]() ЕФЖўДЮКЏЪ§НтЮіЪНЃЎ
ЕФЖўДЮКЏЪ§НтЮіЪНЃЎ
ЪдЬтНтЮіЃК(1)ЖдгкХзЮяЯп![]()
Сюx=0ЃЌЕУЕНy=3ЃЛ
Сюy=0,ЕУЕН![]() ,МД(x3)(x+1)=0ЃЌ
,МД(x3)(x+1)=0ЃЌ
НтЕУЃКx=1Лђx=3ЃЌ
дђA(1,0),B(3,0),C(0,3)ЃЌХзЮяЯпЖдГЦжсЮЊжБЯпx=1ЃЛ
(2)ЂйЩшжБЯпBCЕФКЏЪ§НтЮіЪНЮЊy=kx+bЃЌ
АбB(3,0),C(0,3)ЗжБ№ДњШыЕУЃК![]()
НтЕУЃКk=1ЃЌb3ЃЌ
ЁржБЯпBCЕФНтЮіЪНЮЊy=x+3ЃЌ
ЕБx=1ЪБЃЌy=1+3=2ЃЌ
ЁрE(1,2)ЃЌ
ЕБx=mЪБЃЌy=m+3ЃЌ
ЁрP(m,m+3)ЃЌ
Сю![]() жаx=1ЃЌЕУЕНy=4ЃЌ
жаx=1ЃЌЕУЕНy=4ЃЌ
ЁрD(1,4)ЃЌ
ЕБx=mЪБ,![]()
![]()
ЁрЯпЖЮDE=42=2ЃЌ
Ёп0<m<3ЃЌ
![]()
ЁрЯпЖЮ![]()
СЌНгDF,гЩPFЁЮDEЃЌЕУЕНЕБPF=DEЪБЃЌЫФБпаЮPEDFЮЊЦНааЫФБпаЮЃЌ
гЩ![]() ЕУЕНm=2Лђm=1(ВЛКЯЬтвт,ЩсШЅ)ЃЌ
ЕУЕНm=2Лђm=1(ВЛКЯЬтвт,ЩсШЅ)ЃЌ
дђЕБm=2ЪБЃЌЫФБпаЮPEDFЮЊЦНааЫФБпаЮЃЛ
ЂкСЌНгBF,ЩшжБЯпPFгыxжсНЛгкЕуM,гЩB(3,0),O(0,0)ЃЌПЩЕУOB=OM+MB=3ЃЌ
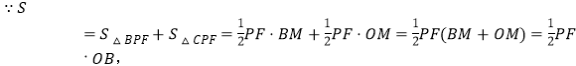
![]()

 жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ
жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ