题目内容
【题目】阅读下面材料:
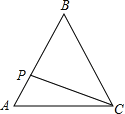
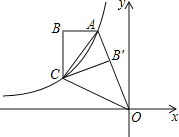
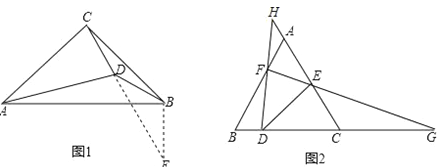
小明遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,AC=BC,在三角形内取一点D,AD=AC,∠CAD=30°,求∠ADB.
小明通过探究发现,∠DAB=∠DCB=15°,BC=AD,这样就具备了一边一角的图形特征,他果断延长CD至点E,使CE=AB,连接EB,造出全等三角形,使问题得到解决.
(1)按照小明思路完成解答,求∠ADB;
(2)参考小明思考问题的方法,解答下列问题:
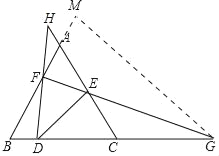
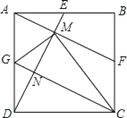
如图2,△ABC中,AB=AC,点D、E、F分别为BC、AC、AB上一点,连接DE,延长FE、DF分别交BC、CA延长线于点G、H,若∠DHC=∠EDG=2∠G.
①在图中找出与∠DEC相等的角,并加以证明;
②若BG=kCD,猜想DE与DG的数量关系并证明.
【答案】(1)135°;(2)①∠HDC=∠DEC;②猜想DG=kDE.
【解析】
(1)根据辅助线证得△DAB≌△BCE,则∠ADB=∠CBE(还不能直接求得,考虑全等的其他等边等角),∠ABD=∠E,BD=BE,得到∠BDE=∠E=∠ABD.考虑引入未知数,设∠CBD=x,则∠E=∠ABD=∠BDE=x+15°,利用∠ABC=∠ABD+∠CBD求得x,再由周角求得结果.
(2)①∠DEC是△DEH的外角,等于∠DHC+∠HDE,而∠DHC=∠EDG,等量代换得∠DEC=∠EDG+∠HDE=∠HDC.
②由条件DHC=∠EDG=2∠G,在FG上方构造2∠G即∠FGM=∠FGD,则∠EDG=∠MGD,令M落在BA延长线上,加上∠B=∠ACB,即得△BGM∽△CDE,有![]() =k.又通过三角形内角和求得∠M=∠HDC,证得△MFG≌△DFG,有MG=DG,得证.
=k.又通过三角形内角和求得∠M=∠HDC,证得△MFG≌△DFG,有MG=DG,得证.
(1)延长CD至点E,使CE=AB,连接EB
∵,∠ACB=90°,AC=BC
∴∠CAB=∠CBA=45°
∵AD=AC,∠CAD=30°
∴BC=AD,∠ACD=∠ADC=![]() =75°,∠DAB=∠CAB﹣∠CAD=15°
=75°,∠DAB=∠CAB﹣∠CAD=15°
∴∠BCD=∠ACB﹣∠ACD=15°
即∠DAB=∠BCD
在△DAB与△BCE中,

∴△DAB≌△BCE(SAS)
∴∠ADB=∠CBE,∠ABD=∠E,BD=BE
∴∠BDE=∠E
设∠CBD=x,则∠ABD=45°﹣x,∠BDE=∠BCD+∠CBD=15°+x
∴∠ABD=∠E=∠BDE=15°+x
∵∠ABC=∠ABD+∠CBD
∴45°=15°+x+x,得:x=15°
∴∠CDB=180°﹣∠BCD﹣∠CBD=180°﹣15°﹣15°=150°
∴∠ADB=360°﹣∠ADC﹣∠CDB=360°﹣75°﹣150°=135°
(2)①∠HDC=∠DEC,证明如下:
∵∠DHC=∠EDG
∴∠HDC=∠HDE+∠EDG=∠HDE+∠DHC=∠DEC
∴∠HDC=∠DEC
②猜想DG=kDE,证明如下:
在FG的上方作∠FGM=∠FGD,使∠FGM的一边与BA延长线交于M
∵∠DHC=∠EDG=2∠FGD
∴∠DHC=∠EDG=∠MGD
∵AB=AC
∴∠B=∠ACB
∴∠M=180°﹣∠B﹣∠MGD=180°﹣∠ACB﹣∠EDC=∠DEC
∴∠M=∠HDC
在△MFG与△DFG中,
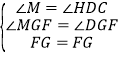
∴△MFG≌△DFG(AAS)
∴MG=DG
∵∠B=∠ACB,∠EDG=∠MGD
∴△BGM∽△CDE
∴![]()
∵BG=kCD
∴![]() =K
=K
∴DG=MG=kDE