题目内容
已知:如图,在四边形ABCD中, AD=BC,∠A、∠B均为锐角.

当∠A=∠B时,则CD与A B的位置关系是CD AB,大小关系是CD AB;
当∠A>∠B时,(1)中C D与A B的大小关系是否还成立,证明你的结论.

当∠A=∠B时,则CD与A B的位置关系是CD AB,大小关系是CD AB;
当∠A>∠B时,(1)中C D与A B的大小关系是否还成立,证明你的结论.
解:
(1)答:如图1,
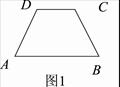
CD∥AB ,CD<AB. …………2分
(2)答:CD<AB还成立. …………3分
证法1:如图2,分别过点D、B作BC、CD的平行线,两线交于F点.
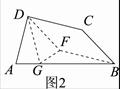
∴ 四边形DCBF为平行四边形.
∴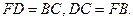
∵ AD=BC,
∴ AD=FD. …………4分
作∠ADF的平分线交AB于G点,连结GF.
∴ ∠ADG=∠FDG.
在△ADG和△FDG中
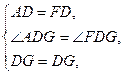
∴ △ADG≌△FDG.
∴ AG=FG. …………5分
∵在△BFG中,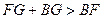 .
.
∴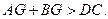 …………6分
…………6分
∴ DC<AB. …………7分
证法2:如图3,分别过点D、B作AB、AD的平行线,两线交于F点.
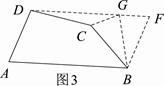
∴ 四边形DABF为平行四边形.
∴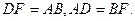
∵ AD=BC,
∴ BC=BF.
作∠CBF的 平分线交DF于G点,连结CG.
平分线交DF于G点,连结CG.
以下同证法1
(1)答:如图1,

CD∥AB ,CD<AB. …………2分
(2)答:CD<AB还成立. …………3分
证法1:如图2,分别过点D、B作BC、CD的平行线,两线交于F点.

∴ 四边形DCBF为平行四边形.
∴
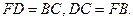
∵ AD=BC,
∴ AD=FD. …………4分
作∠ADF的平分线交AB于G点,连结GF.
∴ ∠ADG=∠FDG.
在△ADG和△FDG中
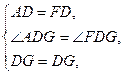
∴ △ADG≌△FDG.
∴ AG=FG. …………5分
∵在△BFG中,
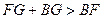 .
. ∴
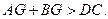 …………6分
…………6分∴ DC<AB. …………7分
证法2:如图3,分别过点D、B作AB、AD的平行线,两线交于F点.

∴ 四边形DABF为平行四边形.
∴
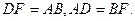
∵ AD=BC,
∴ BC=BF.
作∠CBF的
 平分线交DF于G点,连结CG.
平分线交DF于G点,连结CG.以下同证法1
略

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目


 。
。

 ,AB =" 4" cm.那么,菱形ABCD的对角线AC的长为_____cm
,AB =" 4" cm.那么,菱形ABCD的对角线AC的长为_____cm
 毛
毛