题目内容
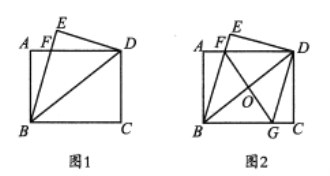
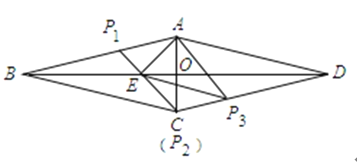
【题目】菱形ABCD中,∠ABC=30°,AC⊥BD,点E在对角线BD上,∠AED=45°,P是菱形上一点,若△AEP是以AE为直角边为直角三角形,则tan∠APE的值为________.
【答案】1或![]() 或
或![]()
【解析】
本题以菱形为题目背景,综合考查菱形的性质,并以动点问题丰富题干,考查分类讨论方式,结合题干信息特殊角度,可通过做辅助线构造特殊直角三角形以满足求解三角函数正切值的前提,继而通过图形性质求解边长比例.
∵菱形ABCD,∠ABC=30°,AC⊥BD
∴∠BAC=75°
连接CE,并延长CE交AB于点P1,如下图所示
当∠AED=45°时,∠BAE=30°,△AEC与△AEP1为直角三角形
在△AEP1中,tan∠AP1E=tan60°=![]()
在△AEC(即△AEP2,此时点P2与点C重合)中,tan∠AP2E=tan45°=1
在△AEP3中,∠EAP3=90°,此时CP1∥AP3
设OA=![]() ,那么EC=AE=
,那么EC=AE=![]() ,EP1=
,EP1=![]()
所以AP3=CP1=![]() +
+![]() ,tan∠AP3E=
,tan∠AP3E=![]() =
=![]() ÷(
÷(![]() +
+![]() )=
)=![]() .
.
综上,tan∠APE的值为1或![]() 或
或![]() .
.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
类别 |
|
|
|
|
|
类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 11 | 20 | 40 |
| 4 |
请你根据以上信息,回答下列问题:
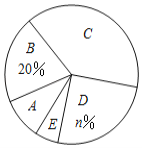
(1)统计表中![]() 的值为_______,统计图中
的值为_______,统计图中![]() 的值为______,
的值为______,![]() 类对应扇形的圆心角为_____度;
类对应扇形的圆心角为_____度;
(2)该校共有1500名学生,根据调查结果,估计该校最喜爱体育节目的学生人数;
(3)样本数据中最喜爱戏曲节目的有4人,其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演,请用树状图或列表求所选2名同学中有男生的概率.