题目内容
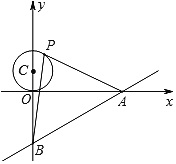
【题目】如图，已知直线y＝
x﹣6与x轴、y轴分别交于A、B两点，点P是以C（0，3）为圆心，3为半径的圆上一动点，连结PA、PB．
（1）求圆心C到直线AB的距离；
（2）求△PAB面积的最大值．
【答案】（1）
；（2）51．
【解析】
（1）求出A、B的坐标，根据勾股定理求出AB．过C作CM⊥AB于M，连接AC，MC的延长线交⊙C于N，则由三角形面积面积法求高，可知圆心C到直线AB的距离；
（2）由（1）中的数据即可求出圆C上点到AB的最大距离，根据面积公式求出即可．
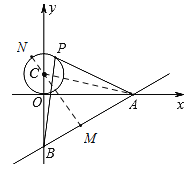
解：解：（1）如图1，过C作
于M，连接AC，MC的延长线交
于N，
由题意：
，
，
，
，
．
，
则由三角形面积公式得，
，
，
，
圆心C到直线AB的距离是
；
（2）由（1）知，圆心C到直线AB的距离是．
则圆C上点到直线
的最大距离是
，
故
面积的最大值是：
．
练习册系列答案
应用题作业本系列答案
相关题目
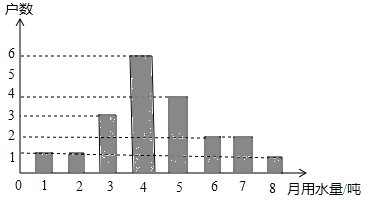
【题目】九（1）班同学为了解某小区家庭月均用水情况（单位：吨），随机调查了该小区部分家庭，并将调查数据进行如下整理：
月均用水量 | 频数（户） | 频率 |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
25 | 2 | 0.04 |
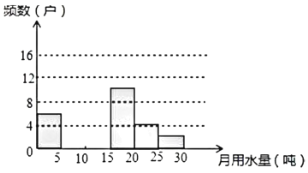
请解答以下问题：
（1）把上面的频数分布表和频数分布直方图补充完整；
（2）若该小区有1000户家庭，根据调查数据估计，该小区月均有水量超过20吨的家庭大约有多少户？
【题目】我市华润生活超市准备一次性购进A、B两种品牌的饮料100箱，此两种饮料每箱的进价和售价如下表所示
设购进A种饮料x箱，且所购进的两种饮料能全部卖出，获得的总利润为y元．
品牌 | A | B |
进价 | 65 | 49 |
售价 | 80 | 62 |
求y关于x的函数关系式；
由于资金周转原因，用于超市购进A、B两种饮料的总费用不超过5600元，并要求获得利润不低于1380元，则从两种饮料箱数上考虑，共有哪几种进货方案？
利润
售价
进价