题目内容
如图,点O是△ABC的内心,过点O作EF∥AB,与AC、BC分别交于点E、F,则( )

A .EF>BE+CF B. EF<BE+CF C.EF=BE+CF D.EF≤BE+CF

A .EF>BE+CF B. EF<BE+CF C.EF=BE+CF D.EF≤BE+CF
C.
试题分析:连接OA、OB.由O是△ABC的内心可知OA、OB分别是∠CAB及∠ABC的平分线,故可得出∠EAO=∠OAB. ∠ABO=∠FBO.再由EF∥AB,可知∠AOE=∠OAB,∠BOF=∠ABO.故可得出∠EAO=∠AOE,∠FBO=∠BOF.故AE=OE,OF=BF,由此即可得出结论.
连接OA、OB.
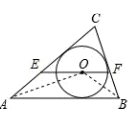
∵O是△ABC的内心
∴OA、OB分别是∠CAB及∠ABC的平分线,
∴∠EAO=∠OAB. ∠ABO=∠FBO.
∵EF∥AB,
∴∠AOE=∠OAB,∠BOF=∠ABO.
∴∠EAO=∠AOE,∠FBO=∠BOF.
∴AE=OE,OF=BF,
∴EF=AE+BF
故选C.
考点: 三角形的内切圆与内心.

练习册系列答案
相关题目




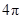 平方米
平方米 平方米
平方米 平方米
平方米 平方米
平方米




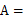 50°,∠
50°,∠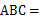 60°,
60°,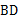 是圆
是圆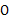 的直径,
的直径,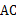 于点
于点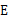 ,连结
,连结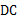 ,则∠
,则∠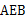 等于( )
等于( )