题目内容
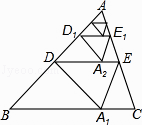
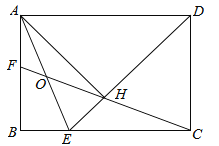
【题目】(3分)如图,在矩形ABCD中,BC=![]() AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O.给出下列命题:
AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O.给出下列命题:
①∠AEB=∠AEH;②DH=![]() EH;③HO=
EH;③HO=![]() AE;④BC﹣BF=
AE;④BC﹣BF=![]() EH.
EH.
其中正确命题的序号是 (填上所有正确命题的序号).
【答案】①③.
【解析】
试题在矩形ABCD中,AD=BC=![]() AB=
AB=![]() CD,∵DE平分∠ADC,∴∠ADE=∠CDE=45°,∵AD⊥DE,∴△ADH是等腰直角三角形,∴AD=
CD,∵DE平分∠ADC,∴∠ADE=∠CDE=45°,∵AD⊥DE,∴△ADH是等腰直角三角形,∴AD=![]() AB,∴AH=AB=CD,∵△DEC是等腰直角三角形,∴DE=
AB,∴AH=AB=CD,∵△DEC是等腰直角三角形,∴DE=![]() CD,∴AD=DE,∴∠AED=67.5°,∴∠AEB=180°﹣45°﹣67.5°=67.5°,∴∠AED=∠AEB,故①正确;
CD,∴AD=DE,∴∠AED=67.5°,∴∠AEB=180°﹣45°﹣67.5°=67.5°,∴∠AED=∠AEB,故①正确;
设DH=1,则AH=DH=1,AD=DE=![]() ,∴HE=
,∴HE=![]() ,∴
,∴![]() HE=
HE=![]() ,故②错误;
,故②错误;
∵∠AEH=67.5°,∴∠EAH=22.5°,∵DH=CH,∠EDC=45°,∴∠DHC=67.5°,∴∠OHA=22.5°,∴∠OAH=∠OHA,∴OA=OH,∴∠AEH=∠OHE=67.5°,∴OH=OE,∴OH=![]() AE,故③正确;
AE,故③正确;
∵AH=DH,CD=CE,在△AFH与△CHE中,∵∠AHF=∠HCE=22.5°,∠FAH=∠HEC=45°,AH=CE,∴△AFH≌△CHE,∴AF=EH,在△ABE与△AHE中,∵AB=AH,∠BEA=∠HEA,AE=AE,∴△ABE≌△AHE,∴BE=EH,∴BC﹣BF=(BE+CE)﹣(AB=AF)=(CD+EH)﹣(CD﹣EH)=2EH,故④错误,故答案为:①③.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目