题目内容
【题目】图1为长方形纸片ABCD，AD=26，AB=22，直线L、M皆为长方形的对称轴．今将长方形纸片沿着L对折后，再沿着M对折，并将对折后的纸片左上角剪下直角三角形，形成一个五边形EFGHI，如图2．最后将图2的五边形展开后形成一个八边形，如图2，且八边形的每一边长恰好均相等．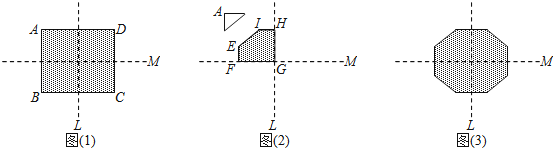
（1）若图2中HI长度为x，请以x分别表示剪下的直角三角形的勾长和股长．
（2）请求出图3中八边形的一边长的数值，并写出完整的解题过程．
【答案】
（1）
解：延长HI与FE相交于点N，如图所示．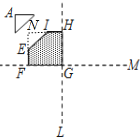
∵HN= 
AD=13，NF= AB=11，HI=EF=x，
∴NI=HN﹣HI=13﹣x，NE=NF﹣EF=11﹣x，
∴剪下的直角三角形的勾长为11﹣x，股长为13﹣x
（2）
解：在Rt△ENI中，NI=13﹣x，NE=11﹣x，
∴EI= 
= 
．
∵八边形的每一边长恰好均相等，
∴EI=2HI=2x= ，
解得：x=5，或x=﹣29（舍去）．
∴EI=2×5=10．
故八边形的边长为10
【解析】（1）延长HI与FE相交于点N，根据折叠的性质找出HN、NF的长，再根据边与边之间的关系即可求出NI、NE的长度，由此即可得出剪下的直角三角形的勾长与股长；
（2）结合（1）的结论利用勾股定理得出线段EI的长，再根据正八边形的性质即可列出关于x的方程，解方程即可得出结论．本题考查了翻折变换中的折叠问题、勾股定理以及解无理方程，解题的关键是：（1）根据边与边之间的关系计算出线段NI、NE的长；（2）列出关于x的无理方程．本题属于基础题，难度不大，解决该题型题目时，巧妙的利用勾股定理列出关于x的方程是关键．
【考点精析】利用翻折变换（折叠问题）对题目进行判断即可得到答案，需要熟知折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
