题目内容
【题目】如图,在平面直角坐标系xOy中,已知直线AC的解析式为y=﹣![]() x+1,直线AC交x轴于点C,交y轴于点A.
x+1,直线AC交x轴于点C,交y轴于点A.
(1)若等边△OBD的顶点D与点C重合,另一顶点B在第一象限内,直接写出点B的坐标;
(2)过点B作x轴的垂线l,在l上是否存在一点P,使得△AOP的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)试在直线AC上求出到两坐标轴距离相等的所有点的坐标.

【答案】(1)B(2,2![]() );(2)点P的坐标为(2,
);(2)点P的坐标为(2,![]() );(3)在直线AC上求出到两坐标轴距离相等的点的坐标为(
);(3)在直线AC上求出到两坐标轴距离相等的点的坐标为(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
【解析】分析:如图,在平面直角坐标系xOy中,已知直线AC的解析式为y=﹣![]() x+1,直线AC交x轴于点C,交y轴于点A.
x+1,直线AC交x轴于点C,交y轴于点A.
(1)若等边△OBD的顶点D与点C重合,另一顶点B在第一象限内,直接写出点B的坐标;
(2)过点B作x轴的垂线l,在l上是否存在一点P,使得△AOP的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)试在直线AC上求出到两坐标轴距离相等的所有点的坐标.
详解:(1)在y=﹣![]() x+1中,令y=0可求得x=4,
x+1中,令y=0可求得x=4,
∴D(4,0),
过B作BE⊥x轴于点E,如图1,
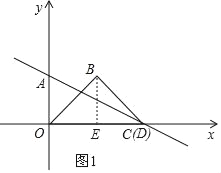
∵△OBD为等边三角形,
∴OE=![]() OD=2,BE=
OD=2,BE=![]() OB=2
OB=2![]() ,
,
∴B(2,2![]() );
);
(2)∵等边△OBD是轴对称图形,对称轴为l,
∴点O与点C关于直线l对称,
∴直线AC与直线l的交点即为所求的点P,
把x=2代入y=﹣![]() x+1,得y=
x+1,得y=![]() ,
,
∴点P的坐标为(2,![]() );
);
(3)设满足条件的点为Q,其坐标为(m,﹣![]() m+1),
m+1),
由题意可得﹣![]() m+1=m或﹣
m+1=m或﹣![]() m+1=﹣m,
m+1=﹣m,
解得m=![]() 或m=﹣
或m=﹣![]() ,
,
∴在直线AC上求出到两坐标轴距离相等的点的坐标为(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).

练习册系列答案
相关题目