题目内容
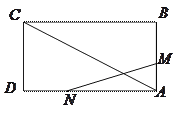
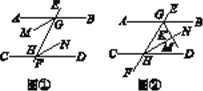
【题目】如图所示,AB∥CD,直线EF分别交AB,CD于点G,H,GM,HN分别为∠BGE和∠DHG的平分线.
(1)试判断GM和HN的位置关系;
(2)如果GM是∠AGH的平分线,(1)中的结论还成立吗?
(3)如果GM是∠BGH的平分线,(1)中的结论还成立吗?如果不成立,你能得到什么结论?

【答案】 (1)GM∥HN.理由见解析;(2)(1)中的结论仍然成立.理由见解析;(3)(1)中的结论不成立.结论:GM⊥HN,理由见解析.
【解析】试题分析:(1)根据平行线的性质可得![]() ,根据角平分线的性质可得
,根据角平分线的性质可得![]() 和
和![]() 的关系,进而
的关系,进而![]() 和
和![]() 的关系,再根据平行线的判定可得
的关系,再根据平行线的判定可得![]() 和
和![]() 的位置关系;
的位置关系;
(2)画出图形,同理根据平行线的性质可得![]() 和
和![]() 的关系,根据角平分线的定义和等量代换可得
的关系,根据角平分线的定义和等量代换可得![]() 再根据平行线的判定可得
再根据平行线的判定可得![]() 和
和![]() 的位置关系;
的位置关系;
(3)画出图形,根据两直线平行,同旁内角互补可得![]() 和
和![]() 的关系,根据角平分线的定义和等量代换可求得
的关系,根据角平分线的定义和等量代换可求得![]() 至此得到结论.
至此得到结论.
试题解析: (1)GM∥HN.
理由:∵AB∥CD, ![]()
∵GM,HN分别为∠BGE和∠DHG的平分线,
∴![]()
∴![]()
∴GM∥HN.
(2)(1)中的结论仍然成立.
理由:如图①,∵AB∥CD,
∴![]()
∵GM,HN分别为∠AGH和∠DHG的平分线,
∴![]()
∴![]()
∴GM∥HN.
(3)(1)中的结论不成立.
结论: ![]()
理由:如图②,∵AB∥CD,∴![]()
∵GM,HN分别为∠BGH和∠DHG的平分线,
∴![]()
∴![]()
设GM,HN相交于点K, ![]()
![]()

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目