题目内容
求函数y=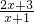 (x>-1)中的y的取值范围.
(x>-1)中的y的取值范围.
解.∵y=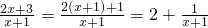
∵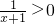
∴y>2
在高中我们将学习这样一个重要的不等式: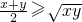 (x、y为正数);此不等式说明:当正数x、y的积为定值时,其和有最小值.
(x、y为正数);此不等式说明:当正数x、y的积为定值时,其和有最小值.
例如:求证:x+ ≥2(x>0)
≥2(x>0)
证明:∵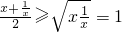
∴x+ ≥2
≥2
利用以上信息,解决以下问题:
(1)求函数:y= 中(x>1),y的取值范围.
中(x>1),y的取值范围.
(2)若x>0,求代数式2x+ 的最小值.
的最小值.
解:(1)y=1+ ,
,
∵x>1,
∴x-1>0,
∴y>1.
(2)∵(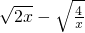 )2≥0,
)2≥0,
∴( )2-2
)2-2 •
•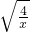 +(
+(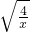 )2≥0,
)2≥0,
∴2x+ ≥2
≥2 •
•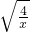 ,
,
2x+ ≥
≥ ,
,
∴2x+ 的最小值为4
的最小值为4 .
.
分析:(1)中,y= =
=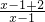 =1+
=1+ ,再结合x>1,即可求出y的取值范围;
,再结合x>1,即可求出y的取值范围;
(2)中,2x+ =(
=(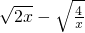 )2+4
)2+4 ≥
≥ .
.
点评:此题是一道材料分析题,给出了求函数取值范围和最小值的方法.此题旨在考查同学们的阅读理解能力
和接受并应用新知识的能力,需对式子进行灵活变形,才能解决问题.
 ,
,∵x>1,
∴x-1>0,
∴y>1.
(2)∵(
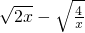 )2≥0,
)2≥0,∴(
 )2-2
)2-2 •
•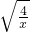 +(
+(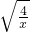 )2≥0,
)2≥0,∴2x+
 ≥2
≥2 •
•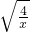 ,
,2x+
 ≥
≥ ,
,∴2x+
 的最小值为4
的最小值为4 .
.分析:(1)中,y=
 =
=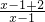 =1+
=1+ ,再结合x>1,即可求出y的取值范围;
,再结合x>1,即可求出y的取值范围;(2)中,2x+
 =(
=(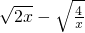 )2+4
)2+4 ≥
≥ .
.点评:此题是一道材料分析题,给出了求函数取值范围和最小值的方法.此题旨在考查同学们的阅读理解能力
和接受并应用新知识的能力,需对式子进行灵活变形,才能解决问题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
 如图,函数y1=k1x+b的图象与函数y2=
如图,函数y1=k1x+b的图象与函数y2=