题目内容
已知一次函数y=(2m-1)x-(n+3),求:(1)当m为何值时,y的值随x的增加而增加;
(2)当n为何值时,此一次函数也是正比例函数;
(3)若m=1,n=2,求函数图象与x轴和y轴的交点坐标;
(4)若m=1,n=2,写出函数关系式,画出图象,根据图象求x取什么值时,y>0.
分析:(1)y的值随x的增加而增加时,2m-1>0;
(2)一次函数为正比例函数时,n+3=0;
(3)若m=1,n=2时,可确定一次函数解析式,再求函数图象与x轴、y轴的交点;
(4)若m=1,n=2时,可确定一次函数解析式,画出函数图象,确定图象与x轴的交点,判断y>0时,x的取值范围.
(2)一次函数为正比例函数时,n+3=0;
(3)若m=1,n=2时,可确定一次函数解析式,再求函数图象与x轴、y轴的交点;
(4)若m=1,n=2时,可确定一次函数解析式,画出函数图象,确定图象与x轴的交点,判断y>0时,x的取值范围.
解答:解:(1)∵y的值随x的增加而增加,
∴2m-1>0;解得m>
;
(2)一次函数为正比例函数时,n+3=0,
解得:n=-3;
(3)若m=1,n=2,一次函数解析式为:y=x-5,
令y=0,得x=5,令x=0,得y=-5,
故函数图象与x轴、y轴的交点为(5,0)(0,-5);
(4)若m=1,n=2,一次函数解析式为:y=x-5,
函数图象如下,
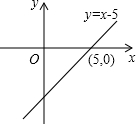
由图象可知,当x>5时,y>0.
∴2m-1>0;解得m>
| 1 |
| 2 |
(2)一次函数为正比例函数时,n+3=0,
解得:n=-3;
(3)若m=1,n=2,一次函数解析式为:y=x-5,
令y=0,得x=5,令x=0,得y=-5,
故函数图象与x轴、y轴的交点为(5,0)(0,-5);
(4)若m=1,n=2,一次函数解析式为:y=x-5,
函数图象如下,

由图象可知,当x>5时,y>0.
点评:本题考查了一次函数图象的性质与解析式的系数的关系,图象的画法及性质.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )
如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )