题目内容
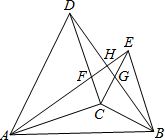 (2011•成华区二模)如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于F,BD分别交CE、AE于点G、H.
(2011•成华区二模)如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于F,BD分别交CE、AE于点G、H.(1)试猜想线段AE和BD之间的关系,并说明理由;
(2)若AC=3,BC=
| 2 |
①求CG:CE的值;②求AB的长.
分析:(1)由于条件可知CD=AC,BC=CE,且可求得∠ACE=∠DCB,所以△ACE≌△DCB,即AE=BD,∠CAE=∠CDB;又因为对顶角相∠AFC=∠DFH,所以∠DHF=∠ACD=90°,即AE⊥BD.
(2)①由∠ACD=∠BCE=90°,∠ACB=135°,可求得∠DCE=45°,又由△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,易证得CD∥BE,则可证得△CDG∽△EBG,然后由相似三角形的对应边成比例,即可求得CG:CE的值;
②过点B作BK⊥AC,交AC的延长线于点K,由∠ACB=135°,即可得△BCK是等腰直角三角形,则可求得BK与CK的长,然后由勾股定理求得AB的长.
(2)①由∠ACD=∠BCE=90°,∠ACB=135°,可求得∠DCE=45°,又由△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,易证得CD∥BE,则可证得△CDG∽△EBG,然后由相似三角形的对应边成比例,即可求得CG:CE的值;
②过点B作BK⊥AC,交AC的延长线于点K,由∠ACB=135°,即可得△BCK是等腰直角三角形,则可求得BK与CK的长,然后由勾股定理求得AB的长.
解答:解:(1)猜测AE=BD,AE⊥BD;理由如下:
∵∠ACD=∠BCE=90°,
∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠DCB,
∵△ACD和△BCE都是等腰直角三角形,
∴AC=CD,CE=CB,
在△ACE与△DCB中,
∵
,
∴△ACE≌△DCB(SAS),
∴AE=BD,
∠CAE=∠CDB;
∵∠AFC=∠DFH,∠FAC+∠AFC=90°,
∴∠DHF=∠ACD=90°,
∴AE⊥BD.
故线段AE和BD的数量是相等,位置是垂直关系.
(2)①∵∠ACD=∠BCE=90°,∠ACB=135°,
∴∠DCE=45°,
∵△ACD和△BCE都是等腰直角三角形,AC=3,BC=
,
∴∠BEC=45°,CD=AC=3,BE=
BC=2,
∴∠DCE=∠BEC,
∴CD∥BE,
∴△CDG∽△EBG,
∴
=
=
,
∴CG:CE=3:5;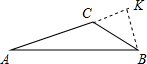
②过点B作BK⊥AC,交AC的延长线于点K,
∵∠ACB=135°,
∴∠BCK=45°,
∴CK=BK=BC•sin45°=
×
=1,
∴AK=AC+CK=3+1=4,
在Rt△ABK中,AB=
=
.
∵∠ACD=∠BCE=90°,
∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠DCB,
∵△ACD和△BCE都是等腰直角三角形,
∴AC=CD,CE=CB,
在△ACE与△DCB中,
∵
|
∴△ACE≌△DCB(SAS),
∴AE=BD,
∠CAE=∠CDB;
∵∠AFC=∠DFH,∠FAC+∠AFC=90°,
∴∠DHF=∠ACD=90°,
∴AE⊥BD.
故线段AE和BD的数量是相等,位置是垂直关系.
(2)①∵∠ACD=∠BCE=90°,∠ACB=135°,
∴∠DCE=45°,
∵△ACD和△BCE都是等腰直角三角形,AC=3,BC=
| 2 |
∴∠BEC=45°,CD=AC=3,BE=
| 2 |
∴∠DCE=∠BEC,
∴CD∥BE,
∴△CDG∽△EBG,
∴
| CG |
| EG |
| CD |
| BE |
| 3 |
| 2 |
∴CG:CE=3:5;

②过点B作BK⊥AC,交AC的延长线于点K,
∵∠ACB=135°,
∴∠BCK=45°,
∴CK=BK=BC•sin45°=
| 2 |
| ||
| 2 |
∴AK=AC+CK=3+1=4,
在Rt△ABK中,AB=
| AK2+BK2 |
| 17 |
点评:此题考查了相似三角形的判定与性质、等腰直角三角形的性质、全等三角形的判定与性质以及勾股定理.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 (2011•成华区二模)小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上(如图),已知∠2=35°,则∠1的度数为( )
(2011•成华区二模)小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上(如图),已知∠2=35°,则∠1的度数为( ) (2011•成华区二模)如图,已知点A是双曲线
(2011•成华区二模)如图,已知点A是双曲线 (2011•成华区二模)如图,在Rt△ABC中,∠ACB=30°,CD=4,BD平分∠ABC,交AC于点D,则点D到BC的距离是( )
(2011•成华区二模)如图,在Rt△ABC中,∠ACB=30°,CD=4,BD平分∠ABC,交AC于点D,则点D到BC的距离是( )