题目内容
 (2011•成华区二模)如图,在Rt△ABC中,∠ACB=30°,CD=4,BD平分∠ABC,交AC于点D,则点D到BC的距离是( )
(2011•成华区二模)如图,在Rt△ABC中,∠ACB=30°,CD=4,BD平分∠ABC,交AC于点D,则点D到BC的距离是( )分析:根据直角三角形两锐角互余求出∠ABC=60°,再根据角平分线的定义求出∠ABD=∠DBC=30°,从而得到∠DBC=∠ACB,然后利用等角对等边的性质求出BD的长度,再根据直角三角形30°角所对的直角边等于斜边的一半求出AD,过点D作DE⊥BC于点E,然后根据角平分线上的点到角的两边的距离相等解答即可.
解答: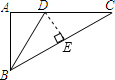 解:∵Rt△ABC中,∠ACB=30°,
解:∵Rt△ABC中,∠ACB=30°,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°,
∴∠DBC=∠ACB,
∴BD=CD=4,
在Rt△ABD中,∵∠ABD=30°,
∴AD=
BD=
×4=2,
过点D作DE⊥BC于点E,
则DE=AD=2.
故选B.
 解:∵Rt△ABC中,∠ACB=30°,
解:∵Rt△ABC中,∠ACB=30°,∴∠ABC=60°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°,
∴∠DBC=∠ACB,
∴BD=CD=4,
在Rt△ABD中,∵∠ABD=30°,
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
过点D作DE⊥BC于点E,
则DE=AD=2.
故选B.
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,30°角所对的直角边等于斜边的一半的性质,以及等角对等边的性质,小综合题,但难度不大,熟记各性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011•成华区二模)小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上(如图),已知∠2=35°,则∠1的度数为( )
(2011•成华区二模)小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上(如图),已知∠2=35°,则∠1的度数为( ) (2011•成华区二模)如图,已知点A是双曲线
(2011•成华区二模)如图,已知点A是双曲线