Question

【题目】已知，如图，△ABC为等边三角形，AE＝CD，AD、BE相交于点P，BQ⊥AD于Q，PQ＝3，PE＝1．

（1）求证：△ABE≌△CAD；

（2）求∠BPQ的度数；

（3）求AD的长．

Answer 1

【答案】（1）见解析；（2）60°；（3）7

【解析】

（1）根据SAS证明△ABE与△CAD全等即可；

（2）根据全等三角形的性质得出∠ABE＝∠CAD，进而解答即可；

（3）根据含30°的直角三角形的性质解答即可．

（1）证明：∵△ABC为等边三角形，

∴AB＝AC，∠BAC＝∠C＝60°，

又∵AE＝CD，

在△ABE与△CAD中，

，

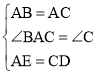∴△ABE≌△CAD（SAS）

（2）由（1）得∠ABE＝∠CAD AD＝BE，

∴∠BPQ＝∠BAD+∠ABE

＝∠BAD+∠CAD

＝60°；

（3）∵BQ⊥AD，∠BPQ＝60°，

∴∠PBQ＝30°，

∴BP＝2PQ＝6，

又∵AD＝BE，

∴BE＝BP+PE＝6+1＝7．