��Ŀ����
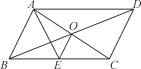
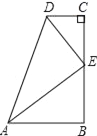
����Ŀ����ͼ����֪������ABCO�У���AB=12��BC=8���Ե�0Ϊԭ�㣬OA��OC���ڵ�ֱ��Ϊy���x�Ὠ��ֱ������ϵ��
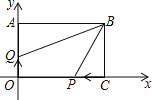
��1����A������Ϊ��0��8����д��B��C��������ꣻ
��2������P��C���������3��λ/����ٶ���CO�����ƶ�����������O������Q��ԭ��O��������2��λ/����ٶ���OA�����ƶ�����������A������P��Q����ͬʱ�������������ƶ������У��ı���OPBQ������Ƿ����仯?�����䣬����ֵ�����仯����仯��Χ��
���𰸡���1��![]() ����2���ı���OPBQ��������ᷢ���仯����ֵʼ��Ϊ48��
����2���ı���OPBQ��������ᷢ���仯����ֵʼ��Ϊ48��
��������
��1�����ݳ����ε����ʿ�֪![]() ���Ӷ�����ȷ��B,C�����ꣻ
���Ӷ�����ȷ��B,C�����ꣻ
��2����P,Q�˶�ʱ��Ϊt���ֱ��ú�t�Ĵ���ʽ��ʾ��![]() ���������
���������![]() ���ɵó��𰸣�
���ɵó��𰸣�
��1�����ı���ABCO�dz����Σ�
��![]() ��
��
��![]() ��
��
![]() ��
��
��2���ı���OPBQ��������ᷢ���仯���������£�
��P,Q�˶�ʱ��Ϊt����![]() ��
��
![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
���ı���OPBQ��������ᷢ���仯����ֵʼ��Ϊ48��

����Ŀ��ij�̵�����ι���![]() ��
��![]() ������Ʒ�������ۣ����ι���ͬһ����Ʒ�Ľ�����ͬ������������±���ʾ��
������Ʒ�������ۣ����ι���ͬһ����Ʒ�Ľ�����ͬ������������±���ʾ��
�������������� | ����������ã�Ԫ�� | ||
|
| ||
��һ�� | 30 | 40 | 3800 |
�ڶ��� | 40 | 30 | 3200 |
��1����![]() ��
��![]() ������Ʒÿ���Ľ��۷ֱ��Ƕ���Ԫ��
������Ʒÿ���Ľ��۷ֱ��Ƕ���Ԫ��
��2���̳�����![]() ����Ʒ��ÿ��30Ԫ���ۣ�
����Ʒ��ÿ��30Ԫ���ۣ�![]() ����Ʒ��ÿ��100Ԫ���ۣ�Ϊ�����г������蹺��
����Ʒ��ÿ��100Ԫ���ۣ�Ϊ�����г������蹺��![]() ��
��![]() ������Ʒ��1000������
������Ʒ��1000������![]() ����Ʒ������������
����Ʒ������������![]() ����Ʒ������4������������������Ľ�����������ȷ���������
����Ʒ������4������������������Ľ�����������ȷ���������