题目内容
【题目】在数轴上点A表示整数a,且![]() ,点B表示a的相反数.
,点B表示a的相反数.
(1)画数轴,并在数轴上标出点A与点B;
(2)点P, Q 在线段AB上,且点P在点Q的左侧,若P, Q两点沿数轴相向匀速运动,出发后经4秒两点相遇. 已知在相遇时点Q比点P多行驶了3个单位,相遇后经1秒点Q到达点P的起始位置. 问点P、Q运动的速度分别是每秒多少个单位;.
(3)在(2)的条件下,若点P从整数点出发,当运动时间为t秒时(t是整数),将数轴折叠,使A点与B点重合,经过折叠P点与Q点也恰好重合,求P点的起始位置表示的数.
【答案】(1)![]() ; (2)点P是
; (2)点P是![]() 个单位/秒;点Q是1个单位/秒;(3)P点的起始位置表示的数为-1或2.
个单位/秒;点Q是1个单位/秒;(3)P点的起始位置表示的数为-1或2.
【解析】
(1)![]() ,找55到65之间的完全平方数可求得
,找55到65之间的完全平方数可求得![]() ,b=-8,在数轴上表示即可;
,b=-8,在数轴上表示即可;
(2)出发4秒后在相遇时点Q比点P多行驶了3个单位,可得关系式![]() .分析可得Q的速度是P的速度的4倍,设P的速度为x单位/秒,则Q的速度为4x单位/秒,可得
.分析可得Q的速度是P的速度的4倍,设P的速度为x单位/秒,则Q的速度为4x单位/秒,可得![]() ,于是可解;
,于是可解;
(3)由(2)可知:P的速度为和Q的速度,于是可求PQ的长. 折点为AB中点是原点,P,Q表示的数互为相反数,据此可解.
解:(1)![]() ,找55到65之间的完全平方数
,找55到65之间的完全平方数
![]() ,所以
,所以![]() ,b=-8
,b=-8

(2)
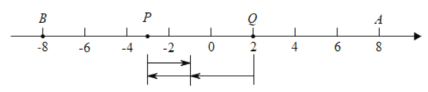
∵出发4秒后在相遇时点Q比点P多行驶了3个单位
∴可得关系式![]()
∵P从初始点到相遇点经过的时间为4s
Q从相遇点到P的初始点经过的时间为1s
∴可得Q的速度是P的速度的4倍
∴设P的速度为x单位/秒,则Q的速度为4x单位/秒
∴![]() ,
,![]()
代入关系式得
![]()
解得 ![]()
则Q的速度为![]() 单位/秒
单位/秒
答:P的速度为![]() 单位/秒,Q的速度为1单位/秒
单位/秒,Q的速度为1单位/秒
(3)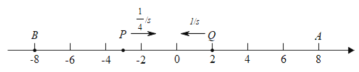
由(2)可知:P的速度为![]() 单位/秒,Q的速度为1单位/秒
单位/秒,Q的速度为1单位/秒
PQ=![]()
由题意,折叠后A,B重合,因此折点为AB中点,即![]()
又∵P,Q运动t秒后,折叠重合,且折点为原点
∴P,Q表示的数互为相反数
设P从y点出发,则Q从(y+5)出发
则P:![]() Q:
Q:![]()
∵P,Q互为相反数
![]()
![]()
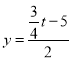
![]()
∵y,t均为整数
且![]()
∴解得![]() 或
或![]()
综上所述:P从-1或2出发满足条件

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案