题目内容
已知二次函数y=x2-4kx+4k2+2k-1在0≤x＜2内有最小值，则k=
- A.-1
- B.
- C.1
- D.-1或1
B
分析：首先把二次函数y=x2-4kx+4k2+2k-1转化成顶点坐标式，找到其对称轴，然后根据在0≤x＜2内有最小值，判断k的取值．
解答：把二次函数y=x2-4kx+4k2+2k-1转化成顶点坐标式为y=（x-2k）2+2k-1，
又知二次函数的开口向上，对称轴为x=2k，
故当x=2k时，二次函数有最小值，
故0≤2k＜2，
故0≤k＜1．
故选B．
点评：本题主要考查二次函数的性质的知识点，解答本题的关键是求出二次函数的对称轴，本题比较简单．
分析：首先把二次函数y=x2-4kx+4k2+2k-1转化成顶点坐标式，找到其对称轴，然后根据在0≤x＜2内有最小值，判断k的取值．
解答：把二次函数y=x2-4kx+4k2+2k-1转化成顶点坐标式为y=（x-2k）2+2k-1，
又知二次函数的开口向上，对称轴为x=2k，
故当x=2k时，二次函数有最小值，
故0≤2k＜2，
故0≤k＜1．
故选B．
点评：本题主要考查二次函数的性质的知识点，解答本题的关键是求出二次函数的对称轴，本题比较简单．
练习册系列答案
相关题目
已知二次函数y=x2+（2a+1）x+a2-1的最小值为0，则a的值是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
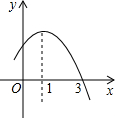已知二次函数y=-x2+2x+m的部分图象如图所示，则关于x的一元二次方程-x2+2x+m=0的解为（ ）| A、x1=1，x2=3 | B、x1=0，x2=3 | C、x1=-1，x2=1 | D、x1=-1，x2=3 |
已知二次函数y=-x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（-1，0），与y轴的交点坐标为（0，3）．