Question

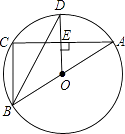
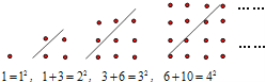
【题目】古希腊著名的毕达哥拉斯学派把1、3、6、10 …这样的数称为“三角形数”，而把1、4、9、16 …这样的数称为“正方形数”．从下图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．用等式表示第100个正方形点阵中的规律_________________.

Answer 1

【答案】4950+5050=1002

【解析】

根据所给的算式结合图形找到一般规律n（n-1）+ n（n+1）= n2，把n=100代入即可求解.

观察图形可得：1=12，1+2+1=22， 1+2+3+2+1=32， 1+2+3+4+3+2+1=42，

∴1+2+3+4+…+（n-1）+n+（n-1）+（n-2）+…+1=n2，

∴ [1+2+3+4+…+（n-1）]+[ n+（n-1）+（n-2）+…+1]=n（n-1）+ n（n+1）= n2，

把n=100代入得，，即4950+5050=1002.

故答案为：4950+5050=1002.