题目内容
【题目】如图1,P是线段AB上的一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G、H分别是AC、AB、BD、CD的中点,顺次连接E、F、G、H.
(1)猜想四边形EFGH的形状,直接回答,不必说明理由;
(2)当点P在线段AB的上方时,如图2,在△APB的外部作△APC和△BPD,其他条件不变,(1)中的结论还成立吗?说明理由;
(3)如果(2)中,∠APC=∠BPD=90°,其他条件不变,先补全图3,再判断四边形EFGH的形状,并说明理由.
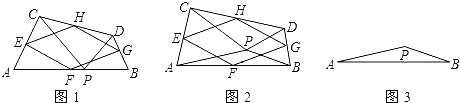
【答案】(1)四边形EFGH是菱形;
(2)成立,理由见解析;
(3)补全图形见解析;四边形EFGH是正方形,理由见解析.
【解析】试题分析:(1)连接AD、BC,利用SAS可判定△APD≌△CPB,从而得到AD=BC,因为EF、FG、GH、EH分别是△ABC、△ABD、△BCD、△ACD的中位线,则可以得到EF=FG=GH=EH,根据四边都相等的四边形是菱形,可推出四边形EFGH是菱形;(2)成立,可以根据四边都相等的四边形是菱形判定;(3)先将图形补充完整,再通过角之间的关系得到∠EHG=90°,已证四边形EFGH是菱形,则四边形EFGH是正方形.
试题解析:(1)四边形EFGH是菱形.
(2)成立.理由:连接AD,BC.
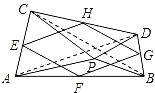
∵∠APC=∠BPD,
∴∠APC+∠CPD=∠BPD+∠CPD.
即∠APD=∠CPB.
又∵PA=PC,PD=PB,
∴△APD≌△CPB(SAS)
∴AD=CB.
∵E、F、G、H分别是AC、AB、BD、CD的中点,
∴EF、FG、GH、EH分别是△ABC、△ABD、△BCD、△ACD的中位线.
∴EF=![]() BC,FG=
BC,FG=![]() AD,GH=
AD,GH=![]() BC,EH=
BC,EH=![]() AD.
AD.
∴EF=FG=GH=EH.
∴四边形EFGH是菱形.
(3)补全图形,如答图.
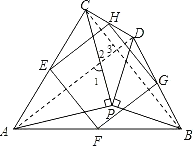
判断四边形EFGH是正方形.
理由:连接AD,BC.
∵(2)中已证△APD≌△CPB.
∴∠PAD=∠PCB.
∵∠APC=90°,
∴∠PAD+∠1=90°.
又∵∠1=∠2.
∴∠PCB+∠2=90°.
∴∠3=90°.
∵(2)中已证GH,EH分别是△BCD,△ACD的中位线,
∴GH∥BC,EH∥AD.
∴∠EHG=90°.
又∵(2)中已证四边形EFGH是菱形,
∴菱形EFGH是正方形.

 习题精选系列答案
习题精选系列答案