Question

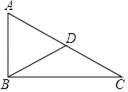
【题目】如图，在△ABC中，点D在AB上，CD＝CB，点E为BD的中点，且EA＝EC，点F为AC的中点，连接EF交CD于点M，连接AM．

（1）求证：EF＝AC；

（2）求线段AM、DM、BC之间的数量关系．

Answer 1

【答案】（1）见解析；（2）BC＝DM+AM．

【解析】

（1）根据等腰三角形三线合一的性质可得CE⊥BD，再根据直角三角形斜边上的中线等于斜边的一半可得EF＝AC；

（2）由等腰三角形的性质可得AF＝FC，EF⊥AC，由“SAS”可得△AFM≌△CFM，可得AM＝CM，可得结论．

（1）证明：∵CD＝CB，点E为BD的中点，

∴CE⊥BD，

∵点F为AC的中点，

∴EF＝AC；

（2）∵AE＝EC，点F是AC中点，

∴AF＝FC，EF⊥AC，

∴∠AFM＝∠CFM，且AF＝FC，MF＝MF，

∴△AFM≌△CFM（SAS）

∴AM＝CM，

∵BC＝CD＝DM+CM＝DM+AM．