题目内容
(2011内蒙古赤峰,16,3分)如图,EF是△ABC的中位线,将△AEF 沿AB
方向平移到△EBD的位置,点D在BC上,已知△AEF的面积为5,则图中阴影部分的面
积为_____________。
方向平移到△EBD的位置,点D在BC上,已知△AEF的面积为5,则图中阴影部分的面
积为_____________。

10
由三角形的中位线的性质,得到EF∥BC,得出三角形相似,进一步利用平移的性质得出S△EBD=5,从而解决问题.
解:∵EF是△ABC的中位线,
∴EF∥BC,
∴△AEF∽△ABC,
∴EF:BC=1:2,
∴S△AEF:S△ABC=1:4,
∵△AEF的面积为5,
∴S△ABC=20,
∵将△AEF沿AB方向平移到△EBD的位置,
∴S△EBD=5,
∴图中阴影部分的面积为:S△ABC-S△EBD-S△AEF=20-5-5=10.
故答案为:10.
此题主要考查了三角形的中位线性质以及平移的性质、三角形相似的判定与性质等知识,根据平移性质得出S△EBD=5是解决问题的关键.
解:∵EF是△ABC的中位线,
∴EF∥BC,
∴△AEF∽△ABC,
∴EF:BC=1:2,
∴S△AEF:S△ABC=1:4,
∵△AEF的面积为5,
∴S△ABC=20,
∵将△AEF沿AB方向平移到△EBD的位置,
∴S△EBD=5,
∴图中阴影部分的面积为:S△ABC-S△EBD-S△AEF=20-5-5=10.
故答案为:10.
此题主要考查了三角形的中位线性质以及平移的性质、三角形相似的判定与性质等知识,根据平移性质得出S△EBD=5是解决问题的关键.

练习册系列答案
相关题目
 ,则梯形的面积是
,则梯形的面积是





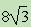 ,求AC的长.
,求AC的长.






 是平行四边形
是平行四边形 的对角线
的对角线 上的点,
上的点, ,请你猜想:线段
,请你猜想:线段 与线段
与线段 有怎样的关系?并对你的猜想加以证明。
有怎样的关系?并对你的猜想加以证明。