题目内容
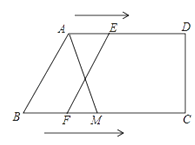
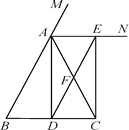
【题目】已知:如图,在△ABC中,AB=AC,点D为BC中点,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.求证:四边形ADCE为矩形.
【答案】见解析
【解析】
试题由AB=AC,AD⊥BC,根据“三线合一”可得AD平分∠BAC,即∠DAC=![]() ∠BAC,再根据AN平分∠CAM,可得∠NAC=
∠BAC,再根据AN平分∠CAM,可得∠NAC=![]() ∠CAM,从而得到∠DAN=90°,再有CE⊥AN,AD⊥BC即可证得结论。
∠CAM,从而得到∠DAN=90°,再有CE⊥AN,AD⊥BC即可证得结论。
在△ABC中,AB=AC,AD⊥BC
∴AD平分∠BAC
∴∠DAC=![]() ∠BAC
∠BAC
又∵AN是ΔABC外角∠CAM的平分线
∴∠NAC=![]() ∠CAM
∠CAM
∴∠DAC+∠NAC=![]() (∠BAC+∠CAM)=90°
(∠BAC+∠CAM)=90°
即∠DAN=90°
又∵CE⊥AN,AD⊥BC
∴∠ADC=∠AEC=90°
∴∠ADC=∠AEC=∠DAN = 90°
∴四边形ADCE是矩形.

练习册系列答案
相关题目