Question

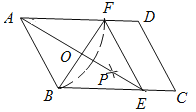
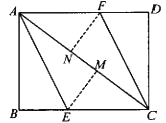
【题目】如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处。
（1）求证：四边形AECF是平行四边形；
（2）若AB=6，AC=10，求四边形AECF的面积。

Answer 1

【答案】（1）证明见解析；（2）30.

【解析】试题分析：（1）首先由矩形的性质和折叠的性质证得AB=CD，AD∥BC，∠ANF=90°，∠CME=90°，易得AN=CM，可得△ANF≌△CME（ASA），由平行四边形的判定定理可得结论；（2）由AB=6，AC=10，可得BC=8，设CE=x，则EM=8-x，CM=10-6=4，在Rt△CEM中，利用勾股定理可解得x，由平行四边形的面积公式可得结果．

试题解析：（1）证明：∵折叠，

∴AM=AB，CN=CD，∠FNC=∠D=90°，∠AME=∠B=90°，

∴∠ANF=90°，∠CME=90°，

∵四边形ABCD为矩形，

∴AB=CD，AD∥BC，

∴AM=CN，

∴AM﹣MN=CN﹣MN，即AN=CM，

在△ANF和△CME中， ，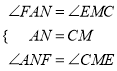

∴△ANF≌△CME（ASA），

∴AF=CE，

又∵AF∥CE，

∴四边形AECF是平行四边形；

（2）解：∵AB=6，AC=10，∴BC=8，

设CE=x，则EM=8﹣x，CM=10﹣6=4，

在Rt△CEM中，（8﹣x）2+42=x2， 解得：x=5，

∴四边形AECF的面积的面积为：ECAB=5×6=30．