Question

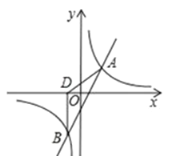
【题目】如图，在平面直角坐标系中，直线与反比例函数的图像在第一象限交于点，在第三象限交于点 ，过 作 轴于，连接 ．

（1）求反比例函数的解析式；

（2）求的面积；

（3）根据图象直接写出时自变量的取值范围．

Answer 1

【答案】（1）；（2）6；（3）或

【解析】

（1）根据点A（2，n）在直线y1=2x-2上求出n的值即可得出反比例函数的解析式；
（2）作AF⊥x轴于点F，由A点坐标可得出AF的长，再取出直线y1=2x-2与x轴的交点E的坐标，根据S△ABD=S△ADE+S△BDE解答即可；
（3）直接根据两函数的图象即可得出y1＞y2时自变量x的取值范围．

（1）直线与反比例函数的图像在第一象限交于点，

∴，

∴，

∴此反比例函数的解析式为；

（2）∵直线与反比例函数的图像在第一象限交于点，

在第三象限交于点，

∴.

∵轴于，

∴，，

作轴于点，

∵，

∴,

∵直线与轴相交于点，

∴，

∴，

∴；

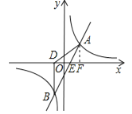
(3) ∵, ,

由函数图像可知，当或是的图像在的上方，

∴当或时，