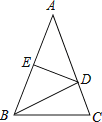Question

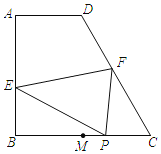
【题目】如图，已知AD∥BC，∠B＝90°，∠C＝60°，BC＝2AD＝4，点M为边BC的中点，点E、F在边AB、CD上运动，点P在线段MC上运动，连接EF、EP、PF，则△EFP的周长最小值为_____．

Answer 1

【答案】2．

【解析】

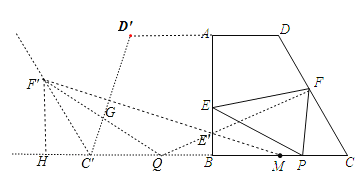
作梯形ABCD关于AB的轴对称图形，将 QC'绕点C'逆时针旋转60°，点Q的对应点为F'，连接F'M，交C' D'于点G，交AB与点E',延长QE'交CD于点F，，则有GE'=FE'，P与Q是关于AB的对称点，当点F'、G、P三点在一条直线上时，△FEP的周长最小即为F'G+GE'+E'P，此时点P与点M重合，F'M为所求长度；过点F'作F'H⊥BC'，M是BC中点，则Q是BC'中点，由已知条件∠B=90°，∠C=60°，BC=2AD=4，可得C'Q=F'C'=2，∠F'C'H=60°，所以F'H=，HC'=7，在Rt△MF'H中，F'M=2.

解：作梯形ABCD关于AB的轴对称图形，将 QC'绕点C'逆时针旋转60°，点Q的对应点为F'，连接F'M，交C' D'于点G，交AB与点E',延长QE'交CD于点F，

则有GE'＝FE'，P与Q是关于AB的对称点，

∴PF＝GQ，

又∵GF'＝GQ，

∴当点F'、G、P三点在一条直线上时，△FEP的周长最小即为F'G+GE'+E'P，

此时点P与点M重合，

∴F'M为所求长度；

过点F'作F'H⊥BC'，

∵M是BC中点，

∴Q是BC'中点，

∵∠B＝90°，∠C＝60°，BC＝2AD＝4，

∴C'Q＝F'C'＝2，∠F'C'H＝60°，

∴F'H＝，HC'＝7，

在Rt△MF'H中，F'M＝2；

∴△FEP的周长最小值为2；

故答案为2；