��Ŀ����
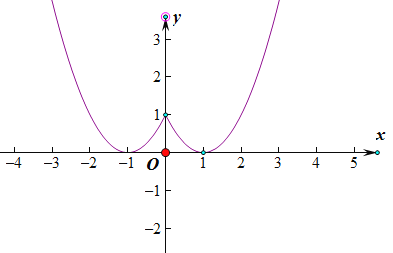
����Ŀ��ij����ѧ��ȤС�顱�Ժ���y��x2��2|x|��1��ͼ������ʽ�����̽����̽������
���£��벹��������
x | �� | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | �� |
y | �� | 4 | 1 | 0 | 1 | 0 | 1 | 4 | �� |
��1�������Ա���x��ȡֵ��Χ��ȫ��ʵ��������е��±������ݱ������ݣ�����ͼ��ʾ
��ƽ��ֱ������ϵ�л����ú�����ͼ��

��2���۲캯��ͼ��д������������������
��_______________________________________��
��_______________________________________��
��3����һ��̽������ͼ���֣�
�ٺ���y��x2��2|x|��1���� x��__ʱ��yȡ��Сֵ��
��СֵΪ__��
����Ϊ����ͼ����x�����������㣬����y��0��
������x2��2|x|��1��0��_________������ȵ�ʵ������
�۷���x2��2|x|��1��1��_______������ȵ�ʵ������
���𰸡� ������ͼ�����y��Գƣ���������Сֵ0�� ����1��x ��0��x��1
ʱ��y��x�����������x ����1��0��x ��1ʱ��y��x���������С�� 1����1 0 2 3
����������������� ![]() ���ݱ���ͼ��.
���ݱ���ͼ��.
![]() �۲�ͼ�ó�����
�۲�ͼ�ó�����![]() ������.
������.
![]() �۲�ͼ��,�������.
�۲�ͼ��,�������.
��������� ![]() ��ͼ��
��ͼ��
![]() �𰸲�Ψһ��������ͼ�����y��Գƣ���������Сֵ0��
�𰸲�Ψһ��������ͼ�����y��Գƣ���������Сֵ0��
��![]() ��
��![]() ʱ��y��x�����������
ʱ��y��x�����������
��![]() ��
��![]() ʱ��y��x���������С��
ʱ��y��x���������С��
![]() �ٹ۲�ͼ��
�ٹ۲�ͼ��![]()
![]() ��
��![]() ʱ��
ʱ�� ![]() ȡ����Сֵ 0 ��
ȡ����Сֵ 0 ��
�ں���ͼ����![]() �����������㣬����
�����������㣬����![]() ����������ȵ�ʵ����.
����������ȵ�ʵ����.
�۷���![]() ��3����ȵ�ʵ������
��3����ȵ�ʵ������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�