Question

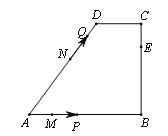
【题目】如图，在四边形ABCD中，AB∥CD，∠B＝90°，AB＝AD＝5，BC＝4，M、N、E分别是AB、AD、CB上的点，AM＝CE＝1，AN＝3，点P从点M出发，以每秒1个单位长度的速度沿折线MB－BE向点E运动，同时点Q从点N，以相同的速度沿折线ND－DC－CE向点E运动，设△APQ的面积为S，运动的时间为t秒，则S与t函数关系的大致图象为（ ）

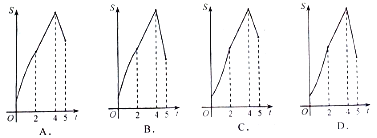
A. A B. B C. C D. D

Answer 1

【答案】D

【解析】试题解析：∵AD=5，AN=3，

∴DN=2，

如图1，过点D作DF⊥AB，

∴DF=BC=4，

在中,AD=5,DF=4,根据勾股定理得,

∴BF=CD=2，

当点Q到点D时用了2s，

∴点P也运动2s，

∴AP=3，即QP⊥AB，

∴只分三种情况：

当时，如图1，

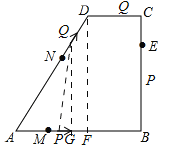
图1

过Q作QG⊥AB,过点D作DF⊥AB,

由题意得，NQ=t，MP=t，

∵AM=1，AN=3，

∴AQ=t+3，

∵AP=t+1，

当t=2时，S=6，

当时，如图2，

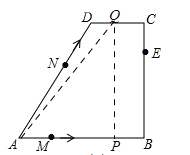
图2

∵AP=AM+t=1+t，

当t=4时，S=8，

当时，如图3，

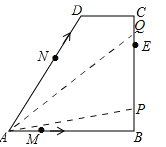
图3

由题意得CQ=t4，PB=t+AMAB=t+15=t4，

∴PQ=BCCQPB=4(t4)(t4)=122t，

当t=5时，S=5，

∴S与t的函数关系式分别是①当t=2时,S=6,

②当t=4时,S=8,③∴当t=5时，S=5，

综合以上三种情况，D正确

故选D.