题目内容
【题目】如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1 , 第二次将△QA1B1变换成△OA2B2 , 第三次将△OA2B2变换成△OA3B3 . 已知A(1,3),A1(2,3),A2(4,3),A3(8,3);B(2,0),B1(4,0),B2(8,0),B3(16,0)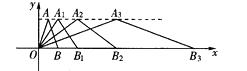
(1)观察每次变换前后三角形的变化规律,若再将△OA3B3变换成△OA4B4 , 则点A4的坐标为 , 点B4的坐标为;
(2)若按第(1)题找到的规律将△OAB进行n次变换,得到△OAnBn , 则点An的坐标为 , 点Bn的坐标为 .
【答案】
(1)(16,3),(32,0)
(2)(2n,3),(2n+1,0)
【解析】(1)∵A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0),
∴A4的横坐标与B3的横坐标相同,纵坐标为3,
∴A4的坐标是(16,3),
B4的横坐标为25=32,纵坐标为0,
∴B4的坐标为(32,0).
所以答案是:(16,3);(32,0).
(2)按第(1)题找到的规律:
An+1的横坐标与Bn的横坐标相同,纵坐标为3,Bn的横坐标为2n+1,纵坐标为0,
∴An的坐标为(2n,3),Bn的坐标为(2n+1,0).
所以答案是:(2n,3);(2n+1,0).
【考点精析】通过灵活运用数与式的规律,掌握先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律即可以解答此题.

练习册系列答案
相关题目