题目内容
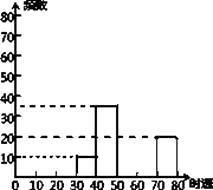
【题目】如图:是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题: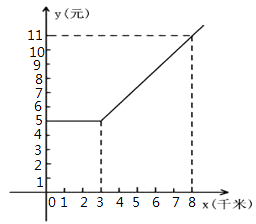
(1)当行使8千米时,收费应为元
(2)从图象上你能获得哪些信息?(请写出2条)
(3)求出收费y(元)与行驶x(千米)(x≥3)之间的函数关系式(直接写出函数关系式)
【答案】
(1)11
(2)解:出租车起步价(3千米内)为5元;
超出3千米,每千米加收1.2元等.
(3)解: 由于x![]() 3时,直线过点(3,5)和(8,11),
3时,直线过点(3,5)和(8,11),
设解析式为:y=kx+b(k![]() 0)
0)
把点(3,5)和(8,11) 代入,得:![]() ,
,
解得:![]() ,
,![]() .
.
【解析】(1)由图象即可确定行驶8千米时的收费;(2)此题答案不唯一,合理即可;(3)由于x![]() 3时,直线过点(3,5)和(8,11), 设解析式为:y=kx+b,利用待定系数法确定函数解析式.
3时,直线过点(3,5)和(8,11), 设解析式为:y=kx+b,利用待定系数法确定函数解析式.
【考点精析】根据题目的已知条件,利用一次函数的图象和性质的相关知识可以得到问题的答案,需要掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
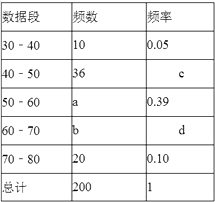
【题目】用甲、乙两种原料配制某种饮料,这两种原料的维生素C含量及购买两种原料的价格如表:
原料 | 甲 | 乙 |
维生素C的含量/(单位/kg) | 600 | 100 |
原料价格/(元/kg) | 8 | 4 |
现配制这种饮料10千克,要求至少含有4200单位的维生素C,且购买甲、乙两种原料的费用不超过72元,求所需甲种原料的质量应满足的范围.