��Ŀ����
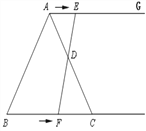
����Ŀ����ͼ���ڵȱ�������ABC����BC=6cm. ����AG//BC����E�ӵ�A����������AG��1cm/s���ٶ��˶���ͬʱ��F�ӵ�B����������BC��2cm/s���ٶ��˶������˶�ʱ��Ϊt(s) ��
��1������EF����EF����AC�ߵ��е�Dʱ����֤����ADE�ա�CDF��
(2)��tΪ��ֵʱ���ı���ACFE��������
��3���Ƿ����ijһʱ��t��ʹ��A��F��C��EΪ������ı����ڽdz���ֱ�ǣ������ڣ����t��ֵ���������ڣ���˵��������
���𰸡���1��֤���������� (2)t=6�� ��3�����ڣ����ɼ�������
����������������1��������õ�AD=CD������AG��BCƽ�У�������ֱ��ƽ���ڴ�����ȵõ����Խ���ȣ�����AAS���ɵ�֤����2�����ı���ACFE�����Σ�����CF=AC=AE=6����E���ٶ����E�˶���ʱ�伴�ɣ���3��������������ǣ���CE��AG����ʱ�ĵ㹹�������Σ�����ֱ�����Σ���AF��BC�����BF�ij��ȼ�ʱ��t��ֵ��
�����������1�� ֤������AG��BC ,��![]() ,��
,��![]() ��AC�ߵ�,��AD=CD
��AC�ߵ�,��AD=CD
�֡�![]() , ���ADE�ա�CDF
, ���ADE�ա�CDF
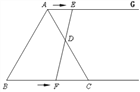
��2���ߵ��ı���ACFE������ʱ����AE=AC=CF=EF,
�������֪��AE=t,CF=2T-6����t=6,
��3�����ı����ڽ���ֱ��ʱ����������������ı���ACFE��ֱ�����Σ���ʱEF��AG�� ��![]() ��CM��AG��M��AM=3���Եõ�AE-CF=AM��
��CM��AG��M��AM=3���Եõ�AE-CF=AM��
��t-(2t-6)=3,��t=3��
��ʱ��C��F�غϣ����������⣬��ȥ��
���ı���![]() ��ֱ�����Σ���ʱAF��BC��
��ֱ�����Σ���ʱAF��BC��
�ߡ�ABC�ǵȱ������Σ�F��BC�е㣬
��2t=3�������飬�������⣬��t=![]() .
.

 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�