题目内容
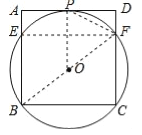
【题目】如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E、F,连接EF.
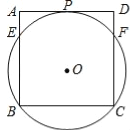
(1)求证:PF平分∠BFD.
(2)若tan∠FBC=![]() ,DF=
,DF=![]() ,求EF的长.
,求EF的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)根据切线的性质得到OP⊥AD,由四边形ABCD的正方形,得到CD⊥AD,推出OP∥CD,根据平行线的性质得到∠PFD=∠OPF,由等腰三角形的性质得到∠OPF=∠OFP,根据角平分线的定义即可得到结论;(2)由∠C=90°,得到BF是⊙O的直径,根据圆周角定理得到∠BEF=90°,推出四边形BCFE是矩形,根据矩形的性质得到EF=BC,根据切割线定理得到PD2=DFCD,于是得到结论.
试题解析:(1)连接OP,BF,PF,
∵⊙O与AD相切于点P,
∴OP⊥AD,
∵四边形ABCD的正方形,
∴CD⊥AD,
∴OP∥CD,
∴∠PFD=∠OPF,
∵OP=OF,
∴∠OPF=∠OFP,
∴∠OFP=∠PFD,
∴PF平分∠BFD;
(2)连接EF,
∵∠C=90°,
∴BF是⊙O的直径,
∴∠BEF=90°,
∴四边形BCFE是矩形,
∴EF=BC,
∵AB∥OP∥CD,BO=FO,
∴OP=![]() AD=
AD=![]() CD,
CD,
∵PD2=DFCD,即(![]() )2=
)2=![]() CD,
CD,
∴CD=4![]() ,
,
∴EF=BC=4![]() .
.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目