题目内容
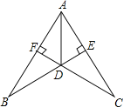
【题目】如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于点D,DE=DF,连接AD.
求证:(1)∠FAD=∠EAD(2)BD=CD.
【答案】(1)、证明过程见解析;(2)、证明过程见解析.
【解析】
试题分析:(1)、根据角平分线的性质可以得出AD平分∠BAC,从而得出答案;(2)、根据题意得出Rt△ADF≌△Rt△ADE,从而得到∠ADF=∠ADE,然后结合∠BDF=∠CDE得出∠ADB=∠ADC,从而说明△ABD≌△ACD,得出答案.
试题解析:(1)、∵BE⊥AC CF⊥AB DE=DF ∴AD是∠BAC的平分线 ∴∠FAD=∠EAD
(2)、∵△ADF与△ADE是直角三角形,DE=DF,AD=AD ∴Rt△ADF≌△Rt△ADE ∴∠ADF=∠ADE
∵∠BDF=∠CDE ∴∠ADF+∠BDF=∠ADF+∠CDE 即∠ADB=∠ADC 又∵∠FAD=∠EAD AD=AD
∴△ABD≌△ACD ∴BD=CD

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目