题目内容
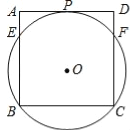
【题目】如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;④AD∥BE;且∠BAD=∠BCD.其中,能推出AB∥DC的条件为________________________.

【答案】②③④
【解析】①∵∠1=∠2,
∴AD∥BC,本选项不合题意;
②∵∠3=∠4,∴AB∥CD,本选项符合题意;
③∵AD∥BE,∴∠BAD+∠B=180,
∵∠D=∠B,
∴∠BAD+∠D=180,
∴AB∥CD,本选项符合题意;
④∵AD∥BE,
∴∠BAD+∠D=180,
∵∠BAD=∠BCD,
∴∠BCD+∠D=180,
∴AB∥CD,本选项符合题意,
则符合题意的选项为②③④。
故答案为:②③④
点睛: 本题考查的是平行线的判定,由角的相等或互补得出直线的平行关系,关键是根据“三线八角”的特征判断这两个角是由那两条直线被哪一条直线所截而成.

练习册系列答案
相关题目