题目内容
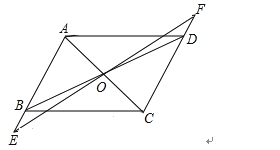
【题目】如图,在ABCD中,点O是AC与BD的交点,过点O的直线EF与AB、CD的延长线分别交于点E、F.
(1)求证:△BOE≌△DOF
(2)当EF⊥AC时,四边形AECF是怎样的特殊四边形?证明你的结论
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴OB=OD,AE∥CF,
∴∠E=∠F,
在△BOE和△DOF中,
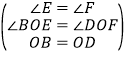 ,
,
∴△BOE≌△DOF(AAS)
(2)
解:当EF⊥AC时,四边形AECF是菱形;理由如下:如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,
又∵△BOE≌△DOF,
∴OE=OF,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形.
【解析】(1)由矩形的性质得出OB=OD,AE∥CF,得出∠E=∠F,由AAS即可证明△BOE≌△DOF;
(2)先由对角线互相平分证明四边形AECF是平行四边形,再由对角线互相垂直,即可得出结论.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分).

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目