题目内容
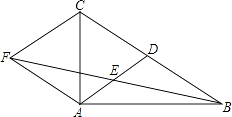
【题目】如图，□ABCD中，E为AD的中点，BE、CD相交于点F.
（1）求证：AB=DF
（2）若△DEF的面积为S1，△BCF的面积为S2，且S12-S2+4=0，求□ABCD的面积.
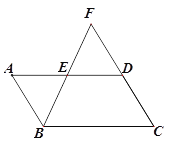
【答案】（1）证明见解析；（2）□ABCD的面积为8.
【解析】分析：(1)由ASA证明△ABE≌△DFE即可求解；（2）通过DE∥BC,得△FED∽△FBC，利用面积比等于相似并的平方求解.
(1) 
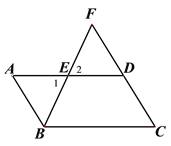
∵四边形ABCD为平行四边形，∴AB∥CD，AB=CD∴∠A=∠EDF
又∵E为AD中点∴AE=DE
在△ABE和△DFE中
,
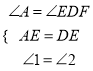∴△ABE≌△DFE（ASA）
∴AB=DF
（2）∵DE∥BC，∴△FED∽△FBC又∵DE=
AD=
BC , ∴
即
，
∴
，∴
，∴
，
又∵△ABE≌△DFE ，∴
练习册系列答案
相关题目
