题目内容
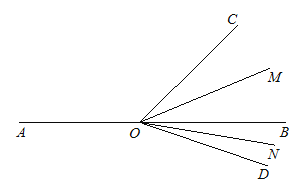
【题目】如图,已知点O为直线AB上一点,射线OC和OD在直线AB的两侧,∠BOC=40°,∠BOD=20°,OM、ON分别平分∠BOC、∠BOD,射线OC以4°/秒的速度绕点O顺时针匀速旋转,射线OD以2°/秒的速度绕点O逆时针匀速旋转.设运动时间为t秒(0<t<100).
(1)运动开始前,∠MON的度数是多少?请写出计算过程.
(2)当t为多少时,∠BOM=8°?请写出计算过程.
(3)当t为多少时,射线OM和射线ON在同一条直线上?请写出计算过程.
【答案】(1)∠MON=30°;(2)t的值为6或14时,∠BOM=8°;(3)t的值为10或70.
【解析】试题分析:(1)由角平分线定义可得:∠MON=![]() ∠COD,由此即可得到结论;
∠COD,由此即可得到结论;
(2)由∠BOM的度数得到∠BOC的度数,解方程40-4t=16或4t-40=16即可得到结论;
(3)分两种情况讨论:①当OM与ON重合时,即OC与OD重合在一起;②当OM与ON互为反向延长线上时.
试题解析:解:(1)∵OM平分∠BOC,∴∠BOM=![]() ∠BOC.
∠BOC.
同理∠BON=![]() ∠BOD,∴∠MON=∠BOM+∠BON=
∠BOD,∴∠MON=∠BOM+∠BON=![]() ∠BOC+
∠BOC+![]() ∠BOD=
∠BOD=![]() ∠COD.
∠COD.
∵∠COD=∠BOC+∠BOD=60°,∴∠MON=30°.
(2)∵∠BOM=![]() ∠BOC=8°,∴∠BOC=16°,∴40-4t=16或4t-40=16,解得t=6或t=14.
∠BOC=8°,∴∠BOC=16°,∴40-4t=16或4t-40=16,解得t=6或t=14.
答:t的值为6或14时,∠BOM=8°.
(3)①当OM与ON重合时,即OC与OD重合在一起,有4t+2t=60, 解得t=10.
②当OM与ON互为反向延长线上时, 有 2t+t=180+30,解得:t=70.
答:t的值为10或70.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目