题目内容
一个多边形的每一个外角都等于72°，这个多边形的对角线条数是________．
5
分析：首先利用多边形的每一个外角的度数求得多边形的边数n，过n边形的一个顶点可画出（n-3）条对角线，那么过n个顶点可以画出n（n-3）条对角线，根据两点确定一条直线，再把所得结果除以2即可求得多边形的对角线的总条数；
解答：360°÷72°=5，则多边形的边数是5．
∴对角线的条数为：
=5（条）．
故答案为5．
点评：本题主要考查了多边形的外角和定理，已知外角求边数的这种方法是需要熟记的内容．三角形的内角和公式及n边形对角线的条数的规律．根据一个顶点处的对角线条数得到n边形对角线的条数的相应规律是解决本题的难点．
分析：首先利用多边形的每一个外角的度数求得多边形的边数n，过n边形的一个顶点可画出（n-3）条对角线，那么过n个顶点可以画出n（n-3）条对角线，根据两点确定一条直线，再把所得结果除以2即可求得多边形的对角线的总条数；
解答：360°÷72°=5，则多边形的边数是5．
∴对角线的条数为：
=5（条）．故答案为5．
点评：本题主要考查了多边形的外角和定理，已知外角求边数的这种方法是需要熟记的内容．三角形的内角和公式及n边形对角线的条数的规律．根据一个顶点处的对角线条数得到n边形对角线的条数的相应规律是解决本题的难点．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
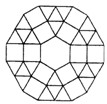10、如图是某广场地面的一部分，地面的中央是一块正六边形的地砖，周围用正三角形和正方形的大理石地砖密铺，从里向外共铺了10层（不包括中央的正六边形地砖），每一层的外边界都围成一个多边形，若中央正六边形的地砖的边长为0.5m，则第10层的外边界所围成的多边形的周长是
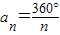，且与每一个外角相等