题目内容
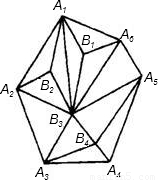
设A1A2A3…An是一个有n个顶点的凸多边形,对每一个顶点Ai(i=1,2,3,…,n),将构成该角的两边分别向外延长至Ai1,Ai2,连接Ai1Ai2得到两个角∠Ai1,∠Ai2,那么所有这些新得到的角的度数的和是
360°
360°
.分析:根据三角形内角和等于180°,凸多边形内角和等于(n-2)•180,将(∠A11+∠A12)+(∠A21+∠A22)+…+(∠An1+∠An2)变形为(∠A11+∠A12+∠A1)+(∠A21+∠A22+∠A2)+…+(∠An1+∠An2+∠An=)-(∠A1+∠A2+∠A3+…+∠An)即可求出所有这些新得到的角的度数的和.
解答:解:n个顶点的凸多边形内角和等于:∠A1+∠A2+∠A3+…+∠An=(n-2)•180,
∠A11+∠A12+∠A1=180 (三角形的内角和).
所以(∠A11+∠A12)+(∠A21+∠A22)+…+(∠An1+∠An2)=180n-180(n-2)=180×2=360.
故答案为:360°.
∠A11+∠A12+∠A1=180 (三角形的内角和).
所以(∠A11+∠A12)+(∠A21+∠A22)+…+(∠An1+∠An2)=180n-180(n-2)=180×2=360.
故答案为:360°.
点评:本题考查了凸多边形内角和的公式和三角形内角和等于180°,解题关键是将各个三角形的内角总和减去凸n多边形内角和.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
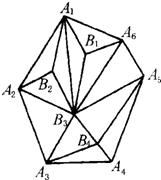 13、设多边形A1A2A3…An中,有m个点B1,B2,B3,…,Bm,连接它们成一张互相毗邻的三角形网(n=6,m=4时的情形如图),称每个小三角形为一个“网眼“,求网中共有
13、设多边形A1A2A3…An中,有m个点B1,B2,B3,…,Bm,连接它们成一张互相毗邻的三角形网(n=6,m=4时的情形如图),称每个小三角形为一个“网眼“,求网中共有