题目内容
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC. 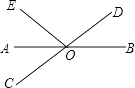
(1)若∠EOC=72°,求∠BOD的度数;
(2)若∠DOE=2∠AOC,判断射线OE,OD的位置关系并说明理由.
【答案】
(1)解:∵OA平分∠EOC,∠EOC=72°,
∴∠AOC= ![]() ∠EOC=36°(角平分线的定义),
∠EOC=36°(角平分线的定义),
∴∠BOD=∠AOC=36°(对顶角相等)
(2)解:OE⊥OD.理由如下:
∵∠DOE=2∠AOC,OA平分∠EOC,
∴∠DOE=∠EOC,
又∠DOE+∠EOC=180°,
∴∠DOE=∠EOC=90°,
∴OE⊥OD(垂直的定义)
【解析】(1)根据角平分线的性质可得∠AOC= ![]() ∠EOC=36°,再根据对顶角相等可得∠BOD的度数;(2)根据题意可得∠DOE=∠EOC,再根据∠DOE+∠EOC=180°可得∠DOE的度数,进而可得OE⊥OD.
∠EOC=36°,再根据对顶角相等可得∠BOD的度数;(2)根据题意可得∠DOE=∠EOC,再根据∠DOE+∠EOC=180°可得∠DOE的度数,进而可得OE⊥OD.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对对顶角和邻补角的理解,了解两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目