题目内容
【题目】如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( ) 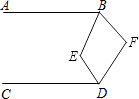
A.∠E=∠F
B.∠E+∠F=180°
C.3∠E+∠F=360°
D.2∠E﹣∠F=90°
【答案】C
【解析】解:过点E作EN∥DC,
∵AB∥CD,
∴AB∥EN∥DC,
∴∠ABE=∠BEN,∠CDE=∠NED,
∴∠ABE+∠CDE=∠BED,
∵∠EBF=2∠ABE,∠EDF=2∠CDE,
∴设∠ABE=x,则∠EBF=2x,设∠CDE=y,则∠EDF=2y,
∵2x+2y+∠BED+∠F=360°,
∴2∠BED+∠BED+∠F=360°,
∴3∠BED+∠F=360°.
故选:C.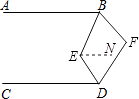
【考点精析】本题主要考查了平行线的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目