题目内容
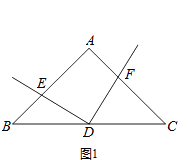
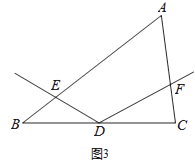
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.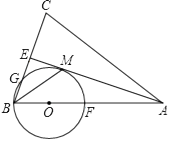
(1)求证:AE为⊙O的切线;
(2)当BC=4,AC=6时,求⊙O的半径;
(3)在(2)的条件下,求线段BG的长.
【答案】
(1)证明:连接OM,如图, 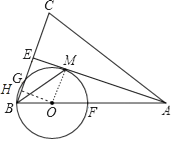
∵BM是∠ABC的平分线,
∴∠OBM=∠CBM,
∵OB=OM,
∴∠OBM=∠OMB,
∴∠CBM=∠OMB,
∴OM∥BC,
∵AB=AC,AE是∠BAC的平分线,
∴AE⊥BC,
∴OM⊥AE,
∴AE为⊙O的切线;
(2)解:设⊙O的半径为r,
∵AB=AC=6,AE是∠BAC的平分线,
∴BE=CE= ![]() BC=2,
BC=2,
∵OM∥BE,
∴△AOM∽△ABE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得r=
,解得r= ![]() ,
,
即设⊙O的半径为 ![]() ;
;
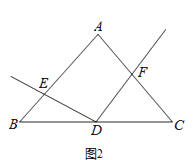
(3)解:作OH⊥BE于H,如图,
∵OM⊥EM,ME⊥BE,
∴四边形OHEM为矩形,
∴HE=OM= ![]() ,
,
∴BH=BE﹣HE=2﹣ ![]() =
= ![]() ,
,
∵OH⊥BG,
∴BH=HG= ![]() ,
,
∴BG=2BH=1.5
【解析】(1)证切线须连半径,再证直线与半径 垂直;(2) 设半径为未知数,利用△AOM∽△ABE构建方程,求出半径;(3)求弦长,须作垂线,得平分,先求一半,再求整体.

练习册系列答案
相关题目