题目内容
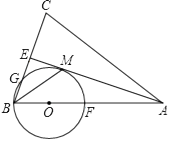
【题目】在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG,DH分别与边AC,BC交于E,F两点.下列结论:①AE+BF=AC,②AE2+BF2=EF2,③S四边形CEDF=![]() S△ABC,④△DEF始终为等腰直角三角形.其中正确的是( )
S△ABC,④△DEF始终为等腰直角三角形.其中正确的是( )

A. ①②③④ B. ①②③ C. ①④ D. ②③
【答案】A
【解析】
连接CD根据等腰直角三角形的性质就可以得出△ADE≌△CDF,就可以得出AE=CF,进而得出CE=BF,就有AE+BF=AC,由勾股定理就可以求出结论.
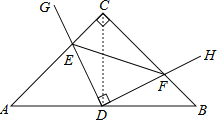
连接CD,∵AC=BC,点D为AB中点,∠ACB=90°,
∴AD=CD=BD=![]() AB.∠A=∠B=∠ACD=∠BCD=45°,∠ADC=∠BDC=90°.
AB.∠A=∠B=∠ACD=∠BCD=45°,∠ADC=∠BDC=90°.
∴∠ADE+∠EDC=90°,
∵∠EDC+∠FDC=∠GDH=90°,
∴∠ADE=∠CDF.
在△ADE和△CDF中,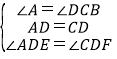
∴△ADE≌△CDF(ASA),
∴AE=CF,DE=DF,S△ADE=S△CDF.
∵AC=BC,
∴AC-AE=BC-CF,
∴CE=BF.
∵AC=AE+CE,
∴AC=AE+BF.
∵DE=DF,∠GDH=90°,
∴△DEF始终为等腰直角三角形.
∵CE2+CF2=EF2,
∴AE2+BF2=EF2.
∵S四边形CEDF=S△EDC+S△EDF,
∴S四边形CEDF=S△EDC+S△ADE=![]() S△ABC.
S△ABC.
∴正确的有①②③④.
故选A.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?