题目内容
【题目】计算:
(1)![]() ;
;
(2)![]()
(3)![]() (代入消元法);
(代入消元法);
(4)![]() (加减消元法)
(加减消元法)
解不等式组,并把解集在数轴上表示出来:
(5)![]() ;
;
(6)
【答案】(1)2-![]() ;(2)
;(2)![]() ;(3)
;(3) ![]() ,(4)
,(4)![]() ;(5)-1<x<2,见解析;(6)x>3,见解析.
;(5)-1<x<2,见解析;(6)x>3,见解析.
【解析】
(1)根据二次根式的性质,绝对值的性质,立方根的定义,进行化简求值即可;
(2)化简绝对值,然后合并同类二次根式即可;
(3)由代入消元法,即可解出方程组的解;
(4)由加减消元法,即可解出方程组的解;
(5)分别求出两个不等式的解集,得到不等式组解集,然后表示在数轴上即可;
(6)分别求出两个不等式的解集,得到不等式组解集,然后表示在数轴上即可.
解:(1)原式=![]() ;
;
(2)原式=![]() ;
;
(3)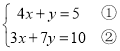
由①得,y=5-4x ③,
把③代入②,得3x+7(5-4x)=10,
解得:x=1,
把x=1代入③,得y=1,
所以方程组的解为![]() ;
;
(4)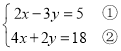 ,
,
①×2+②×3,得16x=64,x=4,
把x=4代入①,得8-3y=5,y=1,
所以方程组的解是![]() ;
;
(5)![]() ,
,
解不等式2x+3>1,得:![]() ,
,
解不等式x-2<0,得:x<2,
则不等式组的解集为:![]() ,
,
将解集表示在数轴上如下:

(6)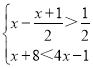
解不等式x-![]() >
>![]() ,得:x>2,
,得:x>2,
解不等式x+8<4x-1,得:x>3,
则不等式组的解集为x>3,
将不等式组的解集表示在数轴上如下:
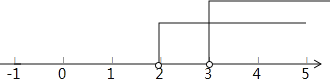 .
.

练习册系列答案
相关题目