题目内容
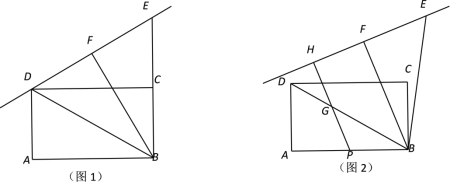
【题目】已知,在矩形ABCD中,BC=2,连接BD,把△ABD绕点B顺时针旋转后得到△FBE,旋转角度小于360°.
(1)如图1,当点E在BC的延长线上,且直线EF过点D,求AB的长.
(2)若AB=4,如图2,取AB边的中点P,过点P作直线EF的垂线PH,垂足为H.
① 若PH交线段BD于点G,当△BPG为等腰三角形时,求BG的长;
② 直接写出PH长的取值范围.
【答案】见解析
【解析】
(1)根据旋转得到∠ABD=∠FBE,再用三线合一性质得∠ABD=∠FBE=∠DBF=30°即可解题.(2)第一问过点P作PM⊥BD,证明△ABD∽△MBP,根据相似比,证明△BPG是等腰三角形,即可求出BG的长,第二问旋转△BAD即可.
(1)由旋转可知∠ABD=∠FBE,BD=BE,
∵四边形ABCD为矩形,
∴∠DAB=∠EFB=∠ABE=90°,
∴BF垂直平分线段DE,
∴∠DBF=∠FBE,
∴∠ABD=∠FBE=∠DBF=30°
在直角三角形DAB中,AD=BC=2,
∴BD=4,AD=2![]()
(2)①如图所示,过点P作PM⊥BD于点M,
∵BC=AD=2,AB=4,P是AB边的中点,
∴BD=2![]() (勾股定理),BP=2,
(勾股定理),BP=2,
又∵∠ABD=∠MBP
∴△ABD∽△MBP
∴![]() =
=![]() ,即
,即![]() =
=![]()
∴MB=![]()
∵△BPG是等腰三角形,PM⊥BD
∴BG=2BM=![]()
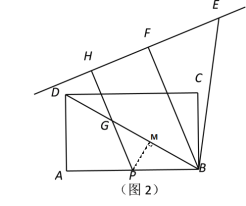
②2![]() ,以点B为旋转中心旋转△BAD,当BF在AB的右侧延长线时,PH最长=BF+BP=6
,以点B为旋转中心旋转△BAD,当BF在AB的右侧延长线时,PH最长=BF+BP=6
当BF与AB重合时,PH最短=AB-BP=2

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目