题目内容
【题目】阅读理解:小明同学进入初二以后,读书越发认真.
在学习“用因式分解法解方程”时,课后习题中有这样一个问题:
下列方程的解法对不对?为什么?![]()
解:![]() 或
或![]() .
.
解得![]() 或
或![]() .
.
所以![]() ,
,![]() .
.
同学们都认为不对,原因:有的说该题的因式分解是错误的;有的说将答案代入方程,方程左右两边不成立,等等.
小明同学除了认为该解法不正确,还给出了一种因式分解的做法,小明同学的做法如下:
取![]() 与
与![]() 的平均值
的平均值![]() ,即将
,即将![]() 与
与![]() 相加再除以2.
相加再除以2.
那么原方程可化为![]() .
.
左边用平方差公式可化为![]() .
.
再移项,开平方可得![]()
请你认真阅读小明同学的方法,并用这个方法推导:
关于![]() 的方程
的方程![]() 的求根公式(此时
的求根公式(此时![]() ).
).
【答案】![]()
【解析】
根据小明同学的做法,将方程的常数项移至右边,二次项系数化为1,提取公因式x,再将方程进行变形,利用平方差公式进行解答即可.
∵![]()
∴![]()
∴![]()
取![]() 与
与![]() 的平均值
的平均值![]() ,即将
,即将![]() 与
与![]() 相加再除以2,即
相加再除以2,即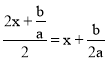
那么原方程可化为:![]()
左边用平方差公式可化为:![]()
再移项可得:![]()
![]()
开平方可得:![]()
![]()
![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目